Wrong result for simple real-valued integral (spurious imaginary part)

Question

There's a question on math SE (question 4879248) about this integral:

    f = (z-a)/Sinh[z-a] (z+a)/Sinh[z+a]
    Integrate[f, {z, -Infinity,Infinity},  Assumptions->{a>0}]

The integrand f is positive and real and free of singularities on the entire real axis, the integral converges, and the answer should simply be this real expression:

    2 a (4 a^2 + Pi^2) Csch[2 a] / 3

For some reason, however, Wolfram Language 13.3.0 Engine includes an imaginary term in it:

                 2                  2
         2 a (4 a  - (6 I) a Pi + Pi ) Csch[2 a]
Out[79]= ---------------------------------------
                            3
(*  (2a(4a^2 - (6I)aPi + Pi^2)Csch[2a])/3  *)

As one can see, it includes a spurious extra term -4I a^2 Pi Csch[2*a]. Why does this go wrong, what can be done about it?

Answer 1

Methods to circumvent the errorprone definite integral algorithms in Mathematica vs 13

The function has the form

 f[z_, a_] = (z - a)/Sinh[z - a] (z + a)/Sinh[z + a] // TrigReduce

$$f(z,a)= 2 \frac{z^2-a^2}{\cosh(2z)-\cosh(2a)}$$

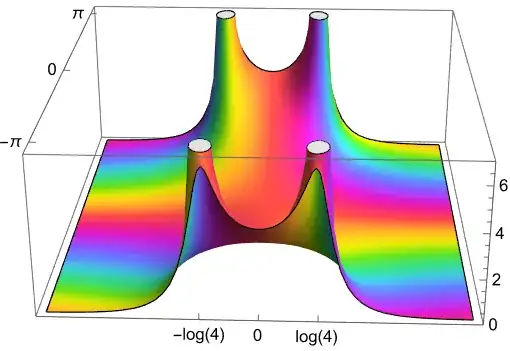
an even function with a cancellation of the singularities of the denominator at $z=\pm a$ on the real line. By $z = x \pm i \pi$ the first four poles are revealed at $\log x =\pm \log a $.

   ComplexPlot3D[
     f[z, Log[4]], {z, -(5 + 1.1 I \[Pi]), (5 + 1.1 I \[Pi])}, 
       PlotRange -> {0, 7}, 
       Ticks -> {{-Log[4], 0, Log[4]}, {-\[Pi], 0, \[Pi]}, Automatic}] 

The direct integration yields an error, possibly by evalution of residues and the difficulties of decomposing the integrand on the shifted contour at $z->z + 3/2 i \pi$ to get a closed contour, closed with imaginary lines at real $z\to \pm \infty+ i y$ and value zero.

So try direct substitution by logs

 f[Log[u], Log[a]]/u // FullSimplify

$$\frac{4 a^2 u \left(\log ^2(a)-\log ^2(u)\right)}{a^4 u^2-a^2 \left(u^4+1\right)+u^2}$$

Just for fun, Mathematica demands a to be complex in order to avoid a possible singularity at $z=\pm 1$, that is removable as we know:

    Assuming[ Im[a] > 0, 
    Integrate[(4 a^2 u Log[a ] ^2)/
            (u^2 + a^4 u^2 - a^2 (1 + u^4)), 
              {u, 0, \[Infinity]}]]

$$\frac{4 a^2 \log ^2(a) (2 \log (a)-i \pi )}{a^4-1}$$

  Assuming[ Im[a] > 0, 
   Integrate[(4 a^2 u Log[u ] ^2)/
            ( u^2 + a^4 u^2 - a^2 (1 + u^4)), 
            {u, 0, \[Infinity]}]]

$$\frac{4 a^2 (\pi +i \log (a)) (\pi +2 i \log (a)) \log (a)}{3-3 a^4}$$

 if[a_] = (4 a^2 Log[a]^2 (-I \[Pi] + 2 Log[a]))/(-1 + a^4) - 
         ( 4 a^2 (\[Pi] + I Log[a]) (\[Pi] + 2 I Log[a]) Log[a])/
            (3 - 3 a^4) //Simplify

$$\frac{4 a^2 \log (a) \left(4 \log ^2(a)+\pi ^2\right)}{3 \left(a^4-1\right)}$$

Confirm

if[E^2.0] --> 1.26394
NIntegrate[f[z, 2], {z, -\[Infinity], \[Infinity]}]   -->  1.26394

Answer 2

$Version

(* "14.0.0 for Mac OS X ARM (64-bit) (December 13, 2023)" *)

Clear["Global`*"]

f[z_] = (z - a)/Sinh[z - a]  (z + a)/Sinh[z + a]

(* -((-a + z) (a + z) Csch[a - z] Csch[a + z]) *)

int1 = Integrate[f[z], {z, -Infinity, Infinity}, Assumptions -> {a > 0}]

(* 2/3 a (4 a^2 - 6 I a π + π^2) Csch[2 a] *)

This has the spurious extra term. However, since f is even

f[-z] == f[z] // Simplify
(* True *)

Then the integral is twice the one-sided integral

int2 = 2*Integrate[f[z], {z, 0, Infinity}, Assumptions -> {a > 0}]
(* 2/3 a (4 a^2 + π^2) Csch[2 a] *)