I don't know the best way to generate these pairs or how to avoid collisions in general and put brackets either top or bottom, but making brackets a bit smaller if there is an intersection seems to work:
drawBracketTop[{i_, j_}, size_ : .5] := Line[{{i, .5}, {i, .5 + size}, {j, .5 + size}, {j, .5}}]
drawBracketBot[{i_, j_}, size_ : .5] := Line[{{i, - .5}, {i, -.5 - size}, {j, - .5 - size}, {j, - .5}}]
intersectQ[pair1_, pair2_] := IntervalIntersection[Interval[pair1], Interval[pair2]] =!= Interval[]
topBotSeparate[pairs_] := Block[{top = {}, bot = {}},
Scan[pair |-> If[
AnyTrue[top, intersectQ[pair, #] &],
AppendTo[bot, pair],
AppendTo[top, pair]
], pairs];
{top, bot}
]
drawBrackets[f_][pairs_]:= FoldPairList[
{state, pair} |-> With[{newSize = If[AnyTrue[state[[2]], intersectQ[pair, #] &], 0.8, 1] state[[1]]}, {f[pair, newSize], {newSize, Append[state[[2]], pair]}}],
{.5, {}},
pairs
]
WickContractions[n_Integer] /; n > 0 && EvenQ[n] := Block[{pairs},
pairs = Select[Select[DuplicateFreeQ] /@ ResourceFunction["ParityPairings"][Range[n]], Length[#] == n / 2 &];
Graphics[{
Table[Text[Style["M", 32, Italic, FontFamily -> "Source Serif Pro"], {i, 0}], {i, n}],
MapAt[drawBrackets[drawBracketBot], {2}] @ MapAt[drawBrackets[drawBracketTop], {1}] @ topBotSeparate[#]
}, PlotRange -> {-1.25, 1.25}] & /@ pairs
]
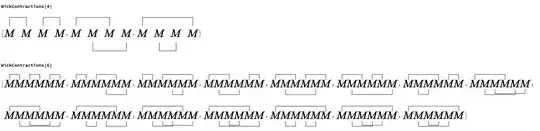
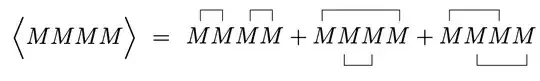









(({{#[[1]], #[[2]]} // Sort, {#[[3]], #[[4]]} // Sort, {#[[5]], #[[6]]} // Sort} // Sort) & /@ Permutations[Range[6]]) // DeleteDuplicates– JimB Mar 19 '24 at 23:38