2

I have a ContourPlot where I have let Mathematica draw the contours automatically. I would like to extract the zmax and zmin contour values that have been determined internally so that I can pass them to ShowLegend to be shown with the color-bar. I am using Mathematica 8. 

Needs["PlotLegends`"]
plTest = ContourPlot[xv^2 + yv^2, {xv, 0, 1}, {yv, 0, 1}, 
  Contours -> 9, ColorFunction -> "Rainbow"];
ShowLegend[plTest, {ColorData["Rainbow"][1 - #1] &, 10, "max", "min", 
  LegendPosition -> {0.6, 0}, BaseStyle -> {FontSize -> 14}}]

I would like the actual zmax and zmin values to appear in the colorbar in the legend instead of the "max" and "min" above. Can someone please help me with this?

There is a similar post: ShowLegend values , but I can't get this to work with ContourPlot type. Thanks.

Community
  • 1
Shrihari
  • 107
  • 2
  • 8

3 Answers3

4

The question refers to my answer to "ShowLegend values" and mentions that it doesn't work with this plot. However, it does work.

The only thing is that for a ContourPlot, one may not want a smooth color gradient in the legend. I actually addressed that in a subsequent answer to "How can I label a ListDensityPlot with a color bar?".

So just follow the instructions in the last link, i.e., load the definitions from the first link and then change colorLegend as given in the second link.

With that, you could then do your plot as follows:

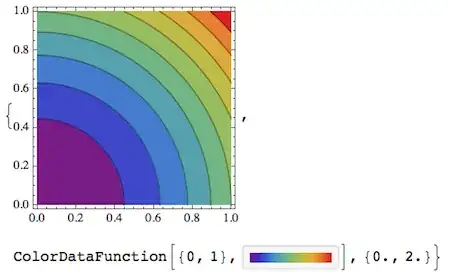
{plot, colors, range} = 
 reportColorRange[
  ContourPlot[xv^2 + yv^2, {xv, 0, 1}, {yv, 0, 1}, Contours -> 9, 
   ColorFunction -> "Rainbow"]]

colors

The last output is the specific answer to the question: it states the range {0, 2} as it was detected by reportColorRange. For legending purposes, it's important to realize that the contour values don't reflect the entire value range because the top and bottom of the range aren't drawn as contours. So post-processing only the drawn contours isn't the correct approach to make a legend. This is why I made the reportColorRange function which monitors what actually is calculated at the time the plot is done.

contour = 
 display[{plot // at[{0, 0}, .8], 
   colorLegend[colors, range, 11] // 
    at[{0.8, 0.1}, Scaled[{.15, 1.5}]]}]

plot

The third argument in colorLegend is the number of tick marks (including the bottom and top-most marks), so in this case for 9 contours it's 11 because the top and bottom of the range aren't drawn as contours.

Community
  • 1
Jens
  • 97,245
  • 7
  • 213
  • 499
  • Apologies, @Jens! Yes, as you claim your code indeed works with ContourPlot also. The reason I thought it doesn't work is because of the following peculiar thing: If I write plTest=ContourPlot[...]; reportColorRange[plTest] it does NOT work! However, if I do reportColorRange[ContourPlot[...]] it DOES work. I am puzzled... – Shrihari Aug 14 '13 at 18:33
  • @Shrihari Yes, this is because reportColorRange has to look over Mathematica's shoulder while it's calculating the plot. So you have to always wrap the actual plot command by reportColorRange. When the plot is already done, it's too late to find out all the function values that have actually been encountered (to get the accurate max and min) - because only the function values at which contours are drawn will actually be kept, and that's not the correct min-max range. – Jens Aug 14 '13 at 18:37
  • Ah, I see. Thanks for the nice implementation. It works fine for my actual plots also! – Shrihari Aug 14 '13 at 19:12
  • Jens, based on your own description (and a quick skim) I think this question should be marked as a duplicate of (7531); do you disagree? – Mr.Wizard Aug 14 '13 at 20:37
  • @Mr.Wizard I agree, now that the intention of the question has been fully clarified. – Jens Aug 14 '13 at 21:41
  • @Mr.Wizard I agree that it's been answered before. I had in fact seen the earlier post, but didn't get it to work with ContourPlot. Jens later explained to me that it will work only if the ContourPlot[...] command is passed to the reportColorRange[...] function. Perhaps that can be explicitly stated in the other post if it has not been. – Shrihari Aug 15 '13 at 08:29
2

The key to this is to look at the Graphics object returned by ContourPlot. Since the display is a side effect of formatting, we need to look at the InputForm of the object returned to prevent the formatting kicking in. (You could use FullForm, too, but it is much more difficult to extract meaningful information from it.) So, when you do that you will see something with this form

Graphics[ GraphicsComplex[{pts:{_, _}..},
 {layers:{{_EdgeForm, _RGBColor, GraphicsGroup[{__Polygon}]}..},
  contours:{Tooltip[{_Directive, _Line}, val_]..}}
 ],
 OptionsPattern[]
]

Don't worry if you don't immediately see that, I have been looking at these for a while, so I know how to look for the structures. From there, there are two ways one could conceivably approach getting the z-values used. First, you could extract the colors from the layers, and invert the color function to give you the corresponding z-value. Since "Rainbow" seems like it is a $1-1$ function, this is probably doable. It is not recommended, though, as an easier way exists: extract the values directly from the Tooltip in the contours. Simply,

Cases[plTest, Tooltip[{_Directive, _Line}, val_] :> val, Infinity]
(* {1.8, 1.6, 1.4, 1.2, 1, 0.8, 0.6, 0.4, 0.2} *)
rcollyer
  • 33,976
  • 7
  • 92
  • 191
  • Thanks @rcollyer . Sure enough, it works on this simple example that we have here. But when I try the Cases[...] line of yours on the actual ContourPlot that I have, I get a Null list, The ContourPlot options are all the same as in this simple example. I don't know how to replicate what I am doing in a simple example, since my code is quite long. Any suggestions? – Shrihari Aug 14 '13 at 15:27
  • is that with or without running InputForm? If you've run InputForm, e.g. plTest = ContourPlot[...]//InputForm, then plTest is the input form, not the Graphics object. Without additional info, that is what I can come up with. You may have to look at the InputForm and see how it differs from the form I've described above. – rcollyer Aug 14 '13 at 15:33
  • You're not finding the max and min values of the actually plotted function, just the extremal values of the drawn contours. This is not the same thing. – Jens Aug 14 '13 at 17:54
  • @Jens you are correct that it isn't the min/max values of the function, but it does provide the min/max values of the contours, as specified by the OP. – rcollyer Aug 14 '13 at 18:51
  • I don't think so. He wants the max and min that go into the color bar. The contours are the lines that divide the color bar, not including the extrema. – Jens Aug 14 '13 at 18:58
  • @Jens To quote: "I would like to extract the zmax and zmin contour values ..." which I read as he wants the contour lines. That said, further processing can be employed to turn those values into ranges with associated colors, so I think what I gave was sufficient, if not complete. – rcollyer Aug 14 '13 at 19:05
  • I get a Null list even with InputForm. I would have followed up on what you said, but I am able to get the code from @Jens below to work. Also, he points out his code gives the actual min and max, not just the contours'. So I will go with that. Thanks! – Shrihari Aug 14 '13 at 19:11
  • @Shrihari you should get an empty list running Cases on InputForm. But, I don't understand why you get an empty list on Cases[ContourPlot[...], ...]. – rcollyer Aug 14 '13 at 19:15
  • I don't know why I get Null list on my actual plot, but example plot above works fine. Sorry I was not clear in my initial posting, as @Jens says, it's really the min and max of the data that would be appropriate, not the contours'; but I could have made do with the latter if I had to :) – Shrihari Aug 14 '13 at 19:26
1
ClearAll["Global`*"];
Needs["PlotLegends`"]

f[x_, y_] := x^2 + y^2;
plTest = ContourPlot[f[x, y], {x, 0, 1}, {y, 0, 1}, Contours -> 9, 
         ColorFunction -> "Rainbow"];

raw = Normal@ContourPlot[f[x, y], {x, 0, 1}, {y, 0, 1}, Contours -> 9];
points = Cases[raw, Line[pts_] :> pts, Infinity];
z = Join @@ points /. {x_, y_} :> f[x, y];

ShowLegend[plTest, {ColorData["Rainbow"][1 - #1] &, 10, 
  ToString[Max[z]], ToString[Min[z]], LegendPosition -> {0.6, 0}, 
  BaseStyle -> {FontSize -> 14}}]

Mathematica graphics

reference: This question

Community
  • 1
Nasser
  • 143,286
  • 11
  • 154
  • 359