Let us consider the following integral $$ B_n = \int_0^\infty \prod_{k=1,3,5,\dots}^n\frac{\sin (x/k)}{x/k}dx $$
By definition, Sinc[x] == Sin[x]/x, therefore
B[n_?OddQ] := Integrate[Product[Sinc[x/k], {k, 1, n, 2}], {x, 0, Infinity}]
B /@ Range[1, 13, 2]
{Pi/2, Pi/2, Pi/2, Pi/2, Pi/2, Pi/2, Pi/2}
OK, everything is fine. But...
B[15]
467807924713440738696537864469 Pi/935615849440640907310521750000
What's going on?
As Eckhard wrote in comments B[n] is the n-th Borwein integral.
(The letter B was not accidental :) )
This funny properties of Borwein integrals is related to the Fourier transform of Sinc function
FourierTransform[Sinc[x], x, k]
1/2 Sqrt[Pi/2] (Sign[1 - k] + Sign[1 + k])
Plot[%, {k, -2, 2}, Filling -> 0]
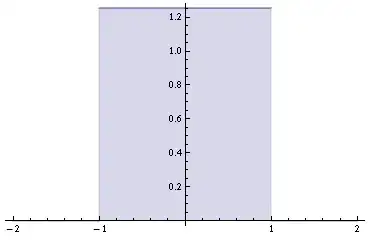
which is the box function. The result is $\pi/2$ while the sum $$ 1/3+1/5+\dots+1/n < 1. $$ If $n \ge 15$ the sum exceeds $1$ and the result becomes
$$ B_n = \frac{\pi}{2} - \pi \bigg(\sum_{k=3,5,\ldots}^n\frac{1}{k} -1\biggr)^\frac{n-1}{2}\prod_{k=3,5,\dots}^n\frac{k}{k-1}. $$
For $n=15$ it is equal to
$$ \frac{467807924713440738696537864469}{935615849440640907310521750000}\pi. $$
As a prank, Jonathan Borwein reported this to Maple, claiming there was a bug in the software. Maple computer scientist Jacques Carette spent 3 days trying to figure out the problem. Then he realized: There was no bug! That's what these integrals really equal!
The Borwein brothers are the same guys who noticed that the integral
$$ \int_0^\infty \cos(2x) \cos(x) \cos(x/2) \cos(x/3) \cos(x/4) \dots dx $$
matches $\pi/8$ up to $43$ decimal places, but is not equal to $\pi/8$. So you've got to be careful with these guys!
N[(467807924713440738696537864469 \[Pi])/ 935615849440640907310521750000 - Pi/2]. – b.gates.you.know.what Sep 18 '13 at 20:29B[15]. – b.gates.you.know.what Sep 18 '13 at 20:39Integrate[..., {x,0,Infinity}]– ssch Sep 18 '13 at 20:42ind = Integrate[( 2027025 Sin[x/15] Sin[x/13] Sin[x/11] Sin[x/9] Sin[x/7] Sin[x/ 5] Sin[x/3] Sin[x])/x^8, x];. – b.gates.you.know.what Sep 18 '13 at 20:46{x,0,b}not{x,0,Infinity}) – ssch Sep 18 '13 at 20:49