Can TreeForm be displayed "sideways"?

Question

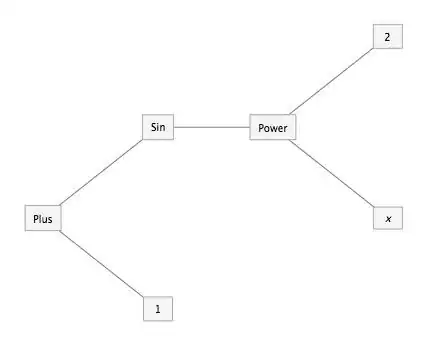
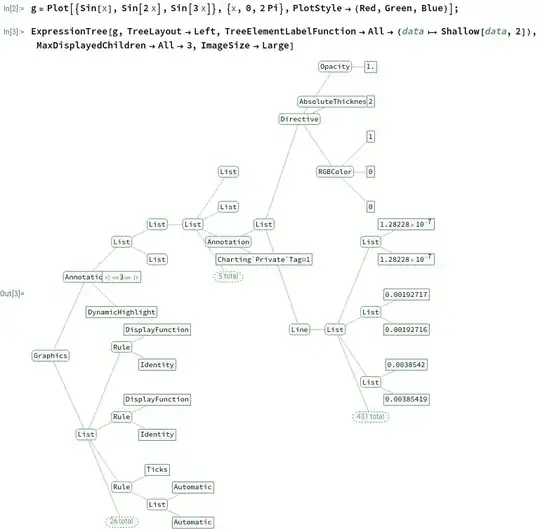
One recurrent problem I'm having with displays generated with TreeForm is that the expressions to be so displayed often at least one level with many (> 20) nodes at, which results in many overlapping labels that obscure each other.¹

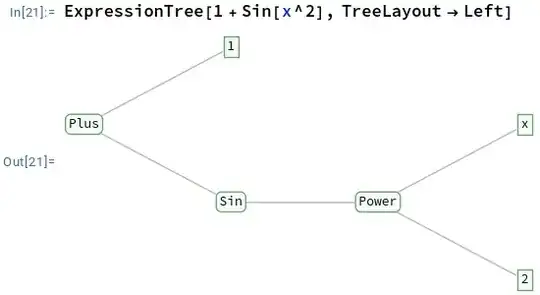
One simple way to mitigate the problem would be to display the same tree "sideways" (i.e., rotated 90 degrees, as would be the case if the display had been generated by a TreePlot command with the Left orientation parameter, for example). Of course, for this strategy to be at all useful, it is necessary that only the geometrical arrangement of the nodes and edges be rotated, not the labels. The latter should remain in the standard "horizontal"/left-to-right/text orientation.

I'm stymied by the fact that the output of TreeForm only looks like a Graphics object, but isn't really one. Is there a way to get Mathematica to return the Graphics object corresponding to the displayed image? Better yet would be to get the equivalent TreePlot command.

EDIT:

¹ For example, the following shows the kind of tree I'm trying to work with:

g = Plot[{Sin[x], Sin[2 x], Sin[3 x]}, {x, 0, 2 Pi},
         PlotStyle -> {Red, Green, Blue}];
TreeForm[g /. x_ /; And @@ NumericQ /@ x :> x[[0]] /. x_[List] :> x]

Answer 1

Here's a possible way, using TreeForm directly, and with VertexRenderingFunction. I think this is what you describe in your second paragraph. I hope this is useful to you

TreeForm[1 + Sin[x^2], 
  VertexRenderingFunction -> (Inset[Panel@Rotate[#2, -π/2], #1] &)] //
    Rotate[#, π/2] &

Answer 2

ExpressionTreePlot (update, thanks to @Belisarius)

The GraphUtilities` package contains a function that will do the trick:

Needs["GraphUtilities`"]
ExpressionTreePlot[1+Sin[x^2], Left]

ExprTreePlot (my original response)

If you do not mind using an undocumented function, then Network`GraphPlot`ExprTreePlot can do the job:

Network`GraphPlot`ExprTreePlot[1+Sin[x^2], Left]

The arguments to this function are:

ExprTreePlot[expr_, orientation_:Top, maxlevel_:Infinity, format_:StandardForm, options___]

Of course, all the usual caveats apply: there is no official support, the feature may be removed from future versions, etc. But it gives us convenient access to all the usual choices for root node placement:

Table[
  Network`GraphPlot`ExprTreePlot[1+Sin[x^2], orientation]
, {orientation , {Left, Right, Top, Bottom, Center}}
] // GraphicsColumn[#, ImageSize -> {200, Automatic}, Frame -> All]&

Recovering the TreePlot

As an alternative, we could extract the TreePlot generated by TreeForm. The complication is that TreeForm is an inert wrapper. The generation of the TreePlot happens when the front-end creates the box form. The good news is that we can use MakeBoxes to extract the TreePlot in held form:

Block[{TreePlot}
, t_TreePlot := Throw @ Hold @ t
; Catch @ MakeBoxes @ TreeForm[1+Sin[x^2]]
]

(*
Hold[TreePlot[
{{"Plus","0","         2\n1 + Sin[x ]"}->{"1","1","1"},...},
Top,
{"Plus","0","         2\n1 + Sin[x ]"},
AlignmentPoint->Center,
AspectRatio->Automatic,
...]]
*)

Beware that the recovered TreePlot expression may use undocumented constructs that generate (harmless) warnings. Such warnings are normally muffled by the front-end's box generation process.

Answer 3

Similar to Pinguin Dirk answer but with the standard style

RotatedTreeForm[x_] := 
  Rotate[TreeForm[x, 
    VertexRenderingFunction -> (Rotate[
        Inset[Framed[Style[#2, "StandardForm", "Output", 
           FontSize -> Scaled[0.1]], Background -> LightYellow, 
          FrameStyle -> GrayLevel[0.5]], #1], -\[Pi]/2] &)], \[Pi]/2];

Cos[Exp[x]] // RotatedTreeForm

Answer 4

Version 12.3 added the experimental function ExpressionTree to convert an expression to a Tree object. Version 13 added the TreeLayout option that can be used to specify the root position. In version 14, the tree is automatically reflected so that the children are always ordered left-to-right or top-to-bottom, as appropriate. Version 13.1 added the TreeElementLabelFunction option which can be used to apply a function to the data to generate the label; e.g. Shallow. And version 13.2 added the MaxDisplayedChildren option to limit the number of children to display.

Here's a simple example of ExpressionTree:

ExpressionTree[1 + Sin[x^2], TreeLayout -> Left]

Here's a more complicated example using these options to manage the complexity:

g = Plot[{Sin[x], Sin[2 x], Sin[3 x]}, {x, 0, 2 Pi}, PlotStyle -> {Red, Green, Blue}];
ExpressionTree[g, TreeLayout -> Left, 
 TreeElementLabelFunction -> All -> (data |-> Shallow[data, 2]), 
 MaxDisplayedChildren -> All -> 3, ImageSize -> Large]

Answer 5

Using the undocumented function SparseArray`ExpressionToTree

expr = 1 + Sin[x^2];
ett = SparseArray`ExpressionToTree[expr];
(* {{Plus,0,1+Sin[x^2]}->{1,1,1},
   {Plus,0,1+Sin[x^2]}->{Sin,2,Sin[x^2]},
   {Sin,2,Sin[x^2]}->{Power,3,x^2},
   {Power,3,x^2}->{x,4,x},
   {Power,3,x^2}->{2,5,2}}*)

edges = ett[[All, All, 1]];
(* {Plus->1,Plus->Sin,Sin->Power,Power->x,Power->2} *)

Graph[edges, 
  VertexLabels -> Placed["Name", {Center, Center}],
  VertexSize -> {"Scaled", .12}, VertexLabelStyle -> 20,
  VertexShapeFunction -> "Rectangle",
  GraphLayout -> {"LayeredEmbedding", "RootVertex" -> edges[[1, 1]],"Orientation" -> Left},
  ImagePadding -> 20, ImageSize -> 600]

Note: This works in Version 9.0.1.0.