Converting expressions to "edges" for use in TreePlot, Graph

Question

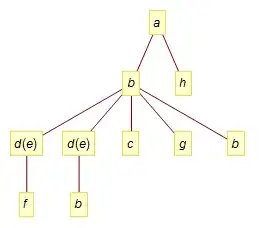
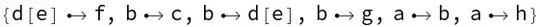This question is similar to this: Nested list to graph. How to "flatten" an arbitrary expression, eg

expr = a[b[c, d[e][f], g], h]

to a list of key-value pairs representing Graph edges of the expression tree:

enter image description here

These can be extracted by applying WReach's exception-based method --> Can TreeForm be displayed “sideways”?:

Block[{TreePlot},
  t_TreePlot := Throw@Hold@t;
  Catch@MakeBoxes@TreeForm[expr]
  ][[1, 1]]

Giving:

{{"a", "0", "a[b[c, d[e][f], g], h]"} -> {"b", "1", 
   "b[c, d[e][f], g]"}, {"b", "1", "b[c, d[e][f], g]"} -> {"c", "2", 
   "c"}, {"b", "1", "b[c, d[e][f], g]"} -> {"d[e]", "3", 
   "d[e][f]"}, {"d[e]", "3", "d[e][f]"} -> {"f", "4", "f"}, {"b", "1",
    "b[c, d[e][f], g]"} -> {"g", "5", "g"}, {"a", "0", 
   "a[b[c, d[e][f], g], h]"} -> {"h", "6", "h"}}

(Why are they cast to String?) Note non-atomic sub-expressions replaced with their Head. Based on the above, and the rule: ({h_, _, _} -> {a_, _, _}) :> ToExpression@h -> ToExpression@ a gives:

{a -> b, b -> c, b -> d[e], d[e] -> f, b -> g, a -> h}

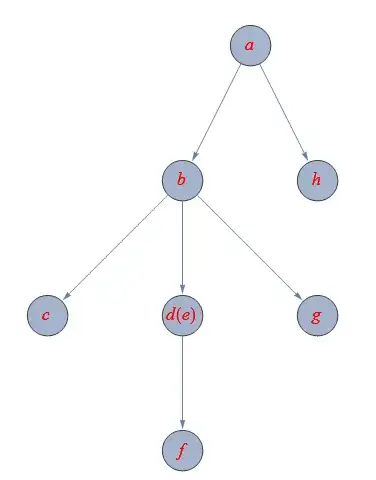
TreeForm is a wrapper around TreePlot. TreePlot[%, VertexLabeling -> True] gives:

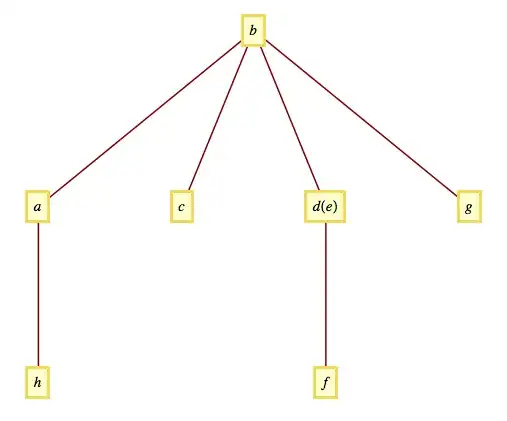
enter image description here

Since the layout is different, TreePlot must be making use of the other components of the output of the Block above.

EDIT:

How do TreeForm and SparseAray`ExpressionToTree (see below) extract these pairs of vertices? "Proof of work" is to extract the position (in the expression) of each vertex along with the edges.

Previously, I asked how to extract these "edges" based on a more restricted example Alternatives ordering affects pattern matching in Cases?. Also tried ReplaceList but don't know how to map it consistently across all levels.

Mr.Wizard · Accepted Answer · 2017-09-12T21:24:50.317

10

Although kguler posted an answer using a nice internal function that does this (almost) directly I find this kind of expression manipulation interesting in itself so I wanted to see what could be done without it.

expr = a[b[c, d[e][f], g], h];

edges =
  Reap[
    Cases[expr, h_[___, c_[___] | c_?AtomQ, ___] /; Sow[h -> c], {0, -1}] 
  ][[2, 1]];

TreePlot[edges, VertexLabeling -> True]

enter image description here

Or for the different layout:

TreePlot[edges, Automatic, Head @ expr, VertexLabeling -> True]

enter image description here

A user asked about non-unique node names. Here is a first attempt at addressing that case.

tree[expr_] :=
  Module[{e2, edges, head},
    e2 = MapIndexed[head, expr, {0, -1}, Heads -> True];
    edges = Reap[
       Cases[e2, (head[h_, x_])[___, 
          head[head[c_, {z__}][___] | c_?AtomQ, {a__}], ___] /; 
         Sow[Annotation[h, x] -> 
           Annotation[c, If[{z} === {}, {a}, {z}]]], {0, -1}]][[2, 1]];
    edges = edges /. head -> Annotation;
    TreePlot[edges, Automatic, edges[[-1, 1]], VertexLabeling -> True]
  ]

a[b[c, d[e][f], g, b, d[e][b]], h] // tree

This very likely has bugs that will need to be addressed as I did it in a hurry and tired, but I think it at least gives us a place to start.

edited Sep 12 '17 at 21:24

answered Jun 27 '14 at 01:30

Mr.Wizard

271,378
34
587
1,371

Thanks, nice use of Sow/Reap, and inner Alternatives. One issue, how to specify Head[expr] as RootVertex? Maybe using a function of Position[expr, h] (in Sow)? – alancalvitti Jun 27 '14 at 21:09
@alancalvitti I'm glad this helps. Regarding "RootVertex" does this do what you want? TreePlot[%, Automatic, Head@expr, VertexLabeling -> True] – Mr.Wizard Jun 28 '14 at 01:11
this answer, as the others here, relies on the nodes being all different. it's not easy to see how to extend it to the case where e.g. b appears twice at different places. one would probably need some temporary node numbering? – user3240588 Sep 12 '17 at 18:14
@user3240588 Good question! I'll have to think about that. – Mr.Wizard Sep 12 '17 at 20:47
@user3240588 Please see my update, and look for cases where it fails so I can try to fix those. – Mr.Wizard Sep 12 '17 at 21:25
@Mr.Wizard it's looking good here: on my examples i get the correct tree structure. no bugs found so far. the ordering within generations seems backwards compared to how TreeForm does it but that's minor. – user3240588 Sep 13 '17 at 08:54

kglr · Answer 2 · 2018-12-09T11:23:58.043

8

An alternative method to WReach's method is to use SparseArray`ExpressionToTree which produces the same output without string wrappers:

expr = a[b[c, d[e][f], g], h];
ett = SparseArray`ExpressionToTree[expr]
(* {{a,0,a[b[c,d[e][f],g],h]}->{b,1,b[c,d[e][f],g]},
    {b,1,b[c,d[e][f],g]}->{c,2,c},
    {b,1,b[c,d[e][f],g]}->{d[e],3,d[e][f]},
    {d[e],3,d[e][f]}->{f,4,f},
    {b,1,b[c,d[e][f],g]}->{g,5,g},
    {a,0,a[b[c,d[e][f],g],h]}->{h,6,h}} *)

edges = ett[[All,All,1]] (* thanks: @Mr.Wizard *)
(* or edges = ett /. Rule[a_, b_] :> Rule[First[a], First[b]];*)
(* {a->b,b->c,b->d[e],d[e]->f,b->g,a->h} *)

Graph[edges, VertexLabels -> Placed["Name", {Center, Center}],
             VertexSize -> .3, VertexLabelStyle -> Directive[Red, Italic, 20],
             ImagePadding -> 20, ImageSize -> 400, 
             GraphLayout -> {"LayeredEmbedding", "RootVertex" -> edges[[1,1]]}]

enter image description here

Update: You can also use GraphComputation`ExpressionGraph:

eg = GraphComputation`ExpressionGraph[expr, VertexSize -> Large, 
   VertexLabelStyle -> Directive[Red, Italic, 20]];
SetProperty[eg,  VertexLabels -> {v_ :> 
    Placed[PropertyValue[{eg, v}, VertexLabels], Center]}]

edited Dec 09 '18 at 11:23

answered Jun 27 '14 at 00:15

kglr

394,356
18
477
896

3

More directly: SparseArray`ExpressionToTree[expr][[All, All, 1]]. Also, thanks for showing me ExpressionToTree! (Again?) – Mr.Wizard Jun 27 '14 at 01:24
@kguler, +1 - btw ETT --> ReleaseHold. But I'm asking how TreeForm (and ETT) convert the expr. I edited my Q to reflect this. – alancalvitti Jun 27 '14 at 18:40
@alancalvitti Is my answer of no interest to you? Are you only interested in the details of the internal implementation and not an equivalent method in top-level code? – Mr.Wizard Jun 27 '14 at 19:37
Yes that works, thank you, I had to test on some expressions of interest. – alancalvitti Jun 27 '14 at 21:06
Since 12.1 ExpressionGraph is now a documented symbol in the System context. https://reference.wolfram.com/language/ref/ExpressionGraph.html – Greg Hurst Feb 01 '24 at 18:41

Szabolcs · Answer 3 · 2018-12-10T17:53:39.260

3

IGraph/M now includes IGExpressionTree:

<<IGraphM`
IGExpressionTree[expr]

GraphQ[%]
(* True *)

edited Dec 10 '18 at 17:53

answered Dec 09 '18 at 11:11

Szabolcs

234,956
30
623
1,263

score 1 · Answer 4 · answered Feb 01 '24 at 08:33

The function Position provides all the information we need to construct the vertex list, edge list and vertex labels to build our own expression graph (in case ExpressionTree or ExpressionGraph is not available in your version):

ClearAll[homeMadeExpressionTree]
Options[homeMadeExpressionTree] = Join[
 {"DownToLevel" -> Automatic, "VertexLabeling" -> Automatic, 
  "RootPosition" -> Top}, 
 Options[Graph]];
homeMadeExpressionTree[$expr_, opts : OptionsPattern[]] := Module[
   {$el, $vlbls, 
    $vl = Position[$expr, _, 
      {0, OptionValue["DownToLevel"] /. Automatic -> Depth@$expr}, 
      Heads -> False]}, 
   $vlbls = Thread[$vl -> Extract[$expr, $vl, 
       Tooltip[If[AtomQ @ #, #, (OptionValue["VertexLabeling"] /.
           {Automatic | Head -> Head, _ -> Identity}) @ #], 
        #, TooltipStyle -> 14] &]];
   $el = Thread[Map[Most] @ # -> #] & @ Most[$vl];
   Graph[$vl, $el, FilterRules[{opts}, Options[Graph]], 
    ImageSize -> Medium, 
    GraphLayout -> {"LayeredEmbedding", "RootVertex" -> {}, 
      "Orientation" -> OptionValue["RootPosition"]}, 
    VertexLabels -> $vlbls]];

Examples:

expr1 = a[b[c, d[e][f], g], h];
homeMadeExpressionTree @ expr1

dsk = Graphics[{RGBColor[1, 0, 0], Disk[{0, 0}]}, ImageSize -> 80];
Row[{homeMadeExpressionTree@dsk, 
     TreeForm[dsk, ImageSize -> Medium]}, Spacer[20]]

expr2 = a[b[c, d[e][f], g, b, d[e][b]], h];
expr3 = HornerForm[1 + x + x^2 + x^3, x];
Grid[{homeMadeExpressionTree[#], 
   homeMadeExpressionTree[#, "RootPosition" -> Left],
   homeMadeExpressionTree[#, "DownToLevel" -> 2, "VertexLabeling" -> Blah]} & /@
  {expr1, expr2, expr3}, 
 Dividers -> All]

score 0 · Answer 5 · answered Feb 01 '24 at 05:54

In versions 13.2+, we can use ExpressionTree as follows:

expr = a[b[c, d[e][f], g], h];
ExpressionTree[expr, "Heads"]

VertexList @ ExpressionTree[expr, "Heads"]

{{c, {1, 1}},   
 {f, {1, 2, 1}},   
 {d[e], {1, 2}},   
 {g, {1, 3}},   
 {b, {1}}, 
 {h, {2}}, 
 {a, {}}}

EdgeList @ ExpressionTree[expr, "Heads"]

 {{d[e], {1, 2}} \[DirectedEdge] {f, {1, 2, 1}},   
  {b, {1}} \[DirectedEdge] {c, {1, 1}},   
  {b, {1}} \[DirectedEdge] {d[e], {1, 2}},   
  {b, {1}} \[DirectedEdge] {g, {1, 3}},   
  {a, {}} \[DirectedEdge] {b, {1}},   
  {a, {}} \[DirectedEdge] {h, {2}}}

%[[All, All, 1]]

WolframLanguageData["ExpressionTree", #] & /@ 
   {"VersionIntroduced", "DateIntroduced"}

score 0 · Answer 6 · answered Jun 26 '14 at 22:01

0

Is this what you are seeking?

expr = a[b[c, d[e][f], g], h]
boxes = ToBoxes@TreeForm[expr]
positions = Cases[boxes, LineBox[{x__}] -> x, Infinity]
nodes =
  Cases[
    boxes,
    StyleBox[x_, __] :> ToExpression@x, Infinity] /. 
      {t_Times :> First@t, Verbatim[HoldForm][x_] -> x}
Rule @@@ Extract[nodes, List /@ positions]

{a -> b, a -> h, b -> c, b -> d, b -> g, d -> f}

answered Jun 26 '14 at 22:01

mfvonh

8,460
27
42

No, for example that doesn't match d[e]. But also, How to extract it directly without using TreeForm? – alancalvitti Jun 26 '14 at 23:15

Converting expressions to "edges" for use in TreePlot, Graph

6 Answers6

Linked