First I want to solve an equation $F(x,y)=0$ for $y$ by supplying a value of $x$. (suppose obtaining the analytic form of $y(x)$ is too difficult) Then I want to plot root $y$ (numerically calculated) as a function of $x$ by using the following:
Plot[y /. FindRoot[.../.{x->x0},{y, 0.2}],{x0, 0, 1}]
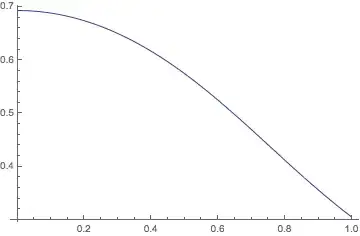
and I got something like the following

I omit ... here since it is terribly complicated. Update: F(x,y) is of the form
$\sum_{n,m}a_{m,n}x^ny^m$
and $m$ and $n$ can be as high as 19, which basically makes Solve impractical.
The result is satisfying except a small number of points near 1.0. Setting another initial starting value of $y$ in FindRoot might be an option but it is very tedious and often I cannot find a value of $y$ that fits the whole range of $x$.
My question is: suppose I stick with the initial value of $y$, is there a way to just eliminate that anomaly point after I Plot the numerical results? Or is there a better way to deal with this kind of numerical problem in general?

FindRoot[...,{x,xstart,xmin,xmax}]and restrict the search to [0,1]. Maybe this helps. – halirutan Oct 23 '13 at 08:16