2

I start with this equation and solve it numerically for $z(x,y)$ in the range $1 < x < 5$ and $1 < y < 5$:

$$ \frac{3}{xyz} - 2x - 3y - 5z = 0 $$

Then using the data points of $z$ above, I want to solve for this special condition:

$$ x + y + z = 0 $$

Then I want to plot a graph of $y(x)$. Everything must be done numerically.

eqn1 = 3/(x y z) - 2 x - 3 y - 5 z   == 3
ContourPlot3D[Evaluate[eqn1], {x, 1, 5}, {y, 1, 5}, {z, 0, -5}]

fulldomain = 
  Table[z /. Solve[eqn1, z, Method -> Reduce], {x, 1, 5, 1}, {y, 1, 5,
     1}] ;

eqn2 = x + y + z  == 0 


special = 
 Table[y /. Solve[eqn2 /. fulldomain, y, Method -> Reduce], {x, 1, 5, 
   1}]

ifun = Interpolation[special]
Plot[ifun[x], {x, 1, 5}, Epilog -> Map[Point, special]]
user44840
  • 421
  • 3
  • 13

1 Answers1

8

There is a difficulty with the statement of the problem. Generally the problem can be solved as shown below. In this case there is a stipulation that $1 < x < 5$ and $1 < y < 5$. Unfortunately the solution to the system does not satisfy these constraints (also shown below).

If we agree to use only numerical techniques and pretend that Solve (nor NSolve) will not produce solutions, then FindRoot is the way to find a single solution. The best way to make an interpolating function for y as a function of x is via NDSolve and a differential-algebraic equation. Below I assume that the equations eqn1 and eqn2 actually define y as a unique function of x. In some systems, this will not be true, and one may have to do more work to determine which branch or branches are to be computed.

We have to find the first point of the intersection with FindRoot. The starting point {x, y, z} = {1, 1, 1} for FindRoot may have to be tweaked for other systems. (It's not a terribly enlightened guess for this specific case, either, but this case is easy for FindRoot.)

eqn1 = 3/(x y z) - 2 x - 3 y - 5 z == 3;
eqn2 = x + y + z == 0;

ic = FindRoot[eqn1 && eqn2 && x == 1, {x, 1}, {y, 1}, {z, 1}]  (* initial values for x, y, z *)

yIFN = NDSolveValue[
  {x'[t] ==  1, {x[1], y[1], z[1]} == ({x, y, z} /. ic),
   {eqn1, eqn2} /. v : (x | y | z) :> v[t]}, y, {t, 1, 5}]
(*
  {x -> 1., y -> 0.890705, z -> -1.8907}

  InterpolatingFunction[{{1., 5.}}, <>]
*)

Plot[yIFN[x], {x, 1, 5}]

Mathematica graphics

Note that by the initial value problem given to NDSolve, x and t are the same.

Note also that 0 < y < 1 -- that is, it does not satisfy the constraint in the problem. Here is another view of the problem in x y z space:

Show[
 ContourPlot3D[
  Evaluate@{eqn1, eqn2}, {x, 0, 5}, {y, 0, 5}, {z, 0, -5}, 
  ContourStyle -> Opacity[0.5], AxesLabel -> Automatic],
 ParametricPlot3D[{x, yIFN[x], -x - yIFN[x]}, {x, 1, 5}, 
  PlotStyle -> {Red, Thickness[0.02]}],
 PlotRange -> All
 ]

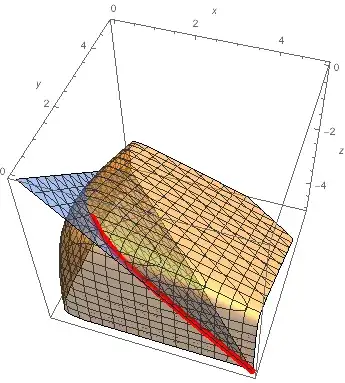
Mathematica graphics

The intersection of the surfaces defined by eqn1 and eqn2 lies outside the region $1 < x < 5$, $1 < y < 5$.

Edit: On setting up NDSolve

To use NDSolveValue, I needed to change simple variables x, y, z to functions x[t], y[t], z[t]. One could simply retype them, but I tend to do it programmatically (if it's convenient -- as you get more familiar with a system, what seem convenient expands). This saves headaches on typos (for me at least) and updating changes to the equations.

Rules and Patterns (->, :>, etc. see What are the most common pitfalls awaiting new users? for a index of such signs) are fundamental objects. Function definitions are stored as rules in a functions DownValues. Many functions return them, such as FindRoot above. The first two links of this paragraph have tutorials and documentation pages for learning about these important objects.

The rules in ic replace the variables x, y, z by the coordinates of the point of intersection of the two surfaces eqn1, eqn2 with the plane x == 1 that was found by FindRoot:

{x'[t] == 1, {x[1], y[1], z[1]} == ({x, y, z} /. ic),...}
(*
  {x'[t] == 1, {x[1], y[1], z[1]} == {1., 0.890705, -1.8907},...}
*)

Since $dx/dt = 1$ and $x(1) = 1$, NDSolveValue will compute the function $x$ to be equal to $x(t) = t$. In other words, t is being used as a dummy variable to represent x along the intersection curve of the two surfaces. One can get more or less of the intersection by changing the integration domain {t, 1, 5} in NDSolveValue to whatever range of x is desired.

To convert the terms of the equations from variables to functions, the following rule was used, which I will display in FullForm:

v : (x | y | z) :> v[t] // FullForm
(*
  RuleDelayed[Pattern[v, Alternatives[x, y, z]], v[t]]
*)

RuleDelayed has the form

pattern :> replacement formula

The Pattern I used has the form

name : pattern object

The name is a variable v that is used in the replacement formula to represent an expression that matches the pattern object. The pattern object in this case is the Alternatives pattern

x | y | z

It matches the expression x, the expression y, or the expression z. The replacement formula is v[t]. So when v matches x, the symbol x is replaced by x[t]; when v matches y, the symbol y is replaced by y[t]; and so on. The second line below in the output shows the complete result:

{{eqn1, eqn2}, {eqn1, eqn2} /. v : (x | y | z) :> v[t]}
(*
  {{-2 x    - 3 y    + 3 / (x    y    z)    - 5 z    == 3, x    + y    + z    == 0},
   {-2 x[t] - 3 y[t] + 3 / (x[t] y[t] z[t]) - 5 z[t] == 3, x[t] + y[t] + z[t] == 0}}
*)
Community
  • 1
Michael E2
  • 235,386
  • 17
  • 334
  • 747
  • why do you put &&x==1 into the list of boundary conditions for FindRoot? – user44840 Sep 09 '14 at 09:34
  • @user44840 Initially because it's an end point of the region $1 < x < 5$ -- I called it the "first point." Afterwards, I realized I assumed there was an endpoint at $x = 1$. In some cases one might have to do some checking to find the endpoint. In other words, FindRoot is finding the point of intersection of your two surfaces and the plane x == 1. – Michael E2 Sep 09 '14 at 11:35
  • I don't really understand the yIFN line of code and in the IC line of code shouldn't there also be && y==1? (since first point also consists of $y=1$) – user44840 Sep 11 '14 at 09:24
  • IC: There are three unknowns so one should use three equations (eqn1, eqn2,x == 1). To add a fourth equation would make the system overdetermined. Ify == 1is added the system becomes inconsistent (no solution). *yIFN:* You might have to be more specific. What's the trouble, differential equations in general, differential-algebraic equations, the first argument,NDSolve? The first argument can be inspected piecemeal. Try evaluating{eqn1, eqn2} /. v : (x | y | z) :> v[t]to see that it replacesxbyx[t]` etc. I'm not sure what to address. – Michael E2 Sep 11 '14 at 12:07
  • What does v : (x | y | z) :> v[t]} mean? I don't understand the syntax at all – user44840 Sep 12 '14 at 08:25
  • @user44840 I've tried to address the issues in the comments in the edit to the answer. Let me know if further clarification is needed. Thanks. – Michael E2 Sep 12 '14 at 12:33
  • I used the same trick here and in the second method here. I used a different approach here. – Michael E2 Sep 12 '14 at 14:28
  • OK I've read through all of the part on Edit, which I understand. However, in the YIFN part of the code, v[t] was never defined earlier (v is just a name for the pattern, right?) – user44840 Sep 15 '14 at 08:37