When does the real part of Zeta vanish on the critical line?

Question

This seems to be a quite a simple problem but I cannot make it work.
I am trying to find all values within a given range for which the real part of the Zeta function vanishes on the line: $\;z=\frac{1}{2} + i\;y$.

Given the following plot:

Plot[Re[ Zeta[ 1/2 + I t]], {t, 14, 14.6}]

I would like to get the values: $14.13...\;, 14.5....$.

Answer 1

When symbolically solving transcendental equations, one should appropriately use Solve or Reduce with adequate logical combinations of equations, inequalities, domain specifications, etc. to get desired results. There are limitations for certain types of equations involving transcendental functions, see e.g. Transcendental Roots. Here is an example which doesn't work in Mathematica 9:

Reduce[ Re[Zeta[x]] == 0 && 14 < Im[x] < 15 && Re[x] == 1/2, x]

Namely, it cannot find roots of the real part of Zeta; nonetheless, we can find symbolic zeros of the Riemann Zeta function:

Solve[Zeta[x] == 0 && 0 < Im[x] < 25 && Re[x] == 1/2, x]

{{x -> ZetaZero[1]}, {x -> ZetaZero[2]}}

Let's use Reduce in another way:

Reduce[ Zeta[ 1/2 + I t] == 0 && 0 <= t <= 250, t]

C[1] ∈ Integers && 1 <= C[1] <= 108 && t == -(1/2) I (-1 + 2 ZetaZero[C[1]])

Here, we provide plot of the real and imaginary part of Zeta on the critical line, in the range 0 < t < 50:

Plot[ Table[ h[ Zeta[ 1/2 + I t]], {h, {Re, Im}}], {t, 0, 50}, 
      Evaluated -> True, AspectRatio -> 1/4, PlotStyle -> Thick, 
      Epilog -> {Red, PointSize[0.007], Point[{Im@ZetaZero[#], 0} & /@ Range[10]]}, 
      ImageSize -> 800, PlotLegends -> Placed["Expressions", {Left, Top}]]

The function ZetaZero is very useful, since one can evaluate its numerical values up to 10^7-th zero (on the other hand, we know there are infinitely many Zeta zeros on the critical line), then one should work with e.g. FindRoot yielding numerical results.

ZetaZero /@ {1, 2, 10^7} // Im // N

{14.1347, 21.022, 4.99238*10^6}

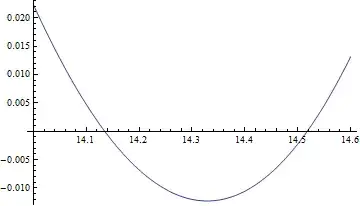
If we are satisfied with numerical values only, we can use FindRoot to get zeros of the real part of Zeta between 14 and 15:

FindRoot[ Re[ Zeta[ 1/2 + I t]], {t, #, 14, 15}]& /@ {14, 14.5}

{{t -> 14.1347}, {t -> 14.5179}}

Zeta[1/2 + I t] /. % // Chop

{0, 0. + 0.31227 I}

Working with FindRoot, it should be useful to localize approximately starting values with ContourPlot like e.g. here.

Answer 2

We can use FindAllCrossings[] to find the roots of $\Re\left(\zeta\left(\frac12+i t\right)\right)$ like so:

FindAllCrossings[Re[Zeta[1/2 + I t]], {t, 10, 30}, WorkingPrecision -> 20]
   {14.134725141734693790, 14.517919628262233651, 20.654044969367919453,
    21.022039638771554993, 25.010857580145688763, 25.491508214625488621,
    29.738510300151580038}

This is of course a superset of the zeroes of $\zeta(s)$, as we can see:

N[Im[ZetaZero[Range[7]]], 20]
   {14.134725141734693790, 21.022039638771554993, 25.010857580145688763,
    30.424876125859513210, 32.935061587739189691, 37.586178158825671257,
    40.918719012147495187}

where for instance we see that $s_2\approx\frac12+14.5179196i$ is a zero of $\Re(\zeta(s))$, but not a zero of $\zeta(s)$.

---

Digression

Back in the day, before ZetaZero[] became built-in, I also used FindAllCrossings[] to find the zeroes of $\zeta(s)$ on the critical line. The function I used for this is the associated Riemann-Siegel function $Z(t)$. Here is how I used it:

FindAllCrossings[RiemannSiegelZ[t], {t, 10, 42}, WorkingPrecision -> 20]

where the results are virtually the same as that of N[Im[ZetaZero[Range[7]]], 20].

The approach is still useful for the more complicated example of the Ramanujan-Dirichlet series $\mathcal{f}(s)$, which is built-in as RamanujanTauL[]. In this scenario, the critical line is at $\Re(s)=6$ instead of $\Re(s)=\frac12$ for $\zeta(s)$. $\mathcal{f}(s)$ also has an associated $Z$ function, built-in as RamanujanTauZ[], that is useful in finding the zeroes of $\mathcal{f}(s)$ on its critical line (see also Keiper's paper for more details):

(* this takes a long time; this function is harder than RiemannSiegelZ[]! *)
FindAllCrossings[RamanujanTauZ[t], {t, 8, 20}, WorkingPrecision -> 20] // Quiet
   {9.2223793999211025235, 13.907549861392134406, 17.442776978234473314,
    19.656513141954961000}

Verify:

RamanujanTauL[6 + I %] // Chop
   {0, 0, 0, 0}