Where did I go wrong with my implementation of finding a plane tangent to a surface?

Question

I am working on finding the plane tangent to a paraboloid at a given point.

My code:

z[x_, y_] := 10 - x^2 - 2 y^2;
Subscript[z, x][x_, y_] := D[z, x];
Subscript[z, y][x_, y_] := D[z, y];
z[1, 2] + Subscript[z, x][1, 2] (x - 1) + 
Subscript[z, x][1, 2] (y - 2)(*The plane tangent equation*)

However, it doesn't work. My question is: where did I go wrong?

Answer 1

I think it's better to avoid subscripting in a problem such as this because subscripting just introduces unnecessary complications.

z[x_, y_] := 10 - x^2 - 2 y^2
zx[x_, y_] := Evaluate @ D[z[x, y], x]
zy[x_, y_] := Evaluate @ D[z[x, y], y]

Evaluate is needed because it is the result of the differentiation that should form the body of the functions zx and zy. Now the tangent plane can be written in accordance with the textbook formula.

tanPlane[x_, y_, x0_, y0_] :=
  Expand[z[x0, y0] + zx[x0, y0] (x - x0) + zy[x0, y0] (y - y0)]

Expand is applied just to make the result look nicer.

tanPlane[x, y, 1, 2]

19 - 2 x - 8 y

The plot may be made with

Plot3D[{z[x, y], tanPlane[x, y, 1, 2]}, {x, -3, 3}, {y, -3, 3}, 
  BoxRatios -> {1, 1, 3},
  Boxed -> False,
  Axes -> None,
  ImageSize -> {200, 300}]

Answer 2

There are two problems and a style issue with the following line:

Subscript[z, x][x_, y_] := D[z, x];

1) You also have x appearing twice on the left hand side, once as a literal symbol x and once as a pattern x_. How is Mathematica supposed to know which value to place in the x on the right hand side?

Subscript[z,x][X_,Y_]:=...

2) In the command D[z,x], you intended z to be a function, but it is just a symbol. The function rule is invoked only if you provide arguments.

Subscript[z,x][X_,Y_]:=D[z[x,y],x]

This is not enough, however, because your intent for the X_,Y_ arguments is to evaluate the result with those values.

Subscript[z,x][X_,Y_]:=D[z[x,y],x]/.{x->X,y->Y}

3) Presumably you will never set OwnValues for x, y, or z so this should be sufficient. I would still prefer to make the function argument a pattern and localize the dummy variables with Module.

Subscript[z_,x][X_,Y_]:=Module[{mX,mY},D[z[mX,mY],mX]/.{mX->X,mY->Y}]

Note that your definition may differ from what you thought it was if you set an OwnValue for x before the definition. Likewise, your definition will not be called if you set/change the OwnValue for x.

Answer 3

The following tries to be as close to your code as possible

Clear[x, y, z]
z[x_, y_] := 10 - x^2 - 2 y^2
Subscript[z, x][x_, y_] = D[z[x, y], x];
Subscript[z, y][x_, y_] = D[z[x, y], y];
z[1, 2] + Subscript[z, x][1, 2] (x - 1) + Subscript[z, y][1, 2] (y - 2)

But I think it is a bad idea to use Subscript in this way.

Answer 4

The principal question, which seems to be why the OP's code does not work, has been answered by Timothy Wofford, but I thought the following alternative to plotting the tangent plane might be appreciated, since it deals with the underlying problem in the question.

The equation of a tangent plane to $z = f(x,y)$, $$z-f(a,b)=f_x(a,b)\;(x-a)+f_y(a,b)\;(y-b)\,,$$ has the same form as the differential $dz$, $$dz = f_x(a,b)\;dx + f_y(a,b)\;dy\,,$$ with finite differences corresponding to the differentials.

This idea is easy to code in Mathematica. The first form of the function tp below is for an equation. Indeed it can even be an equation of the form $F(x,y,z)=0$. It returns the equation of the tangent plane at {a, b, c}. The second form is for a function $f(x,y)$. It returns a linear expression in x and y that can be viewed as representing a function whose graph is the tangent plane. The standard coordinates x, y and z are assumed.

tp[eqn_Equal, {a_, b_, c_}] :=
  Dt[eqn] /. {Dt[x] -> x - a, Dt[y] -> y - b, Dt[z] -> z - c, x -> a, y -> b, z -> c};
tp[expr_, {a_, b_}] :=
  expr + Dt[expr] /. {Dt[x] -> x - a, Dt[y] -> y - b, x -> a, y -> b}

The equation of the tangent plane:

With[{f = 10 - x^2 - 2 y^2, a = 1, b = 2},
 tp[z == f, {x, y, f} /. {x -> a, y -> b}]
 ]
(*  -1 + z == -2 (-1 + x) - 8 (-2 + y) *)

The function whose graph is the tangent plane to f:

With[{f = 10 - x^2 - 2 y^2, a = 1, b = 2},
 tp[f, {a, b}]]
(* 1 - 2 (-1 + x) - 8 (-2 + y) *)

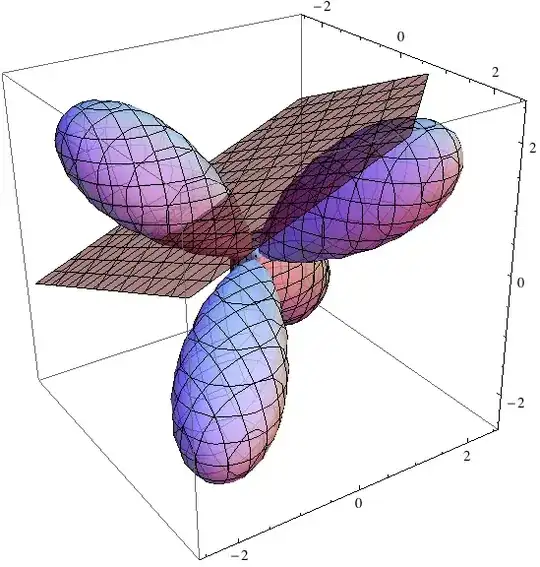
A tangent plane to a surface defined by an equation:

surf = (x^2 + y^2 + z^2)^2 == 18 x y z;
ContourPlot3D[Evaluate@{surf, tp[surf, {1, 1, 2}]},
 {x, -2.5, 2.5}, {y, -2.5, 2.5}, {z, -2.5, 2.5},
 ContourStyle -> {Directive[Opacity[0.8], LightBlue], Directive[Opacity[0.5], Red]}
 ]

Answer 5

As a more general remark, in cases like the above the intention of the author is often to simply have a symbol available that is expressed by a subscripted expression. Mathematica has the Notation package with its function Symbolize available for this purpose, but the documentation of its use and purpose are not easy to find since there seems to be no link to the Tutorial page for the package (it can be found under "Notation, Symbolize, and InfixNotation").

Using Symbolize, rather than resorting to changing the OP's function names into slightly less intuitive forms using things like "zx" rather than Subscript[z, x], the OP could use the subscripted variable names.