5

I have about 1,000,000,000 points, which are the longitudes and latitudes of some places in a city, formatted like this: $(106.1231233,41.43234234)$. I also have about 20,000 points which are the longitudes and latitudes of some special places in this city. For every item in the 1,000,000,000 point data set, I have to compute which point in the 20,000 point data set is the nearest. If I were to compute on a brute-force, one by one basis, it might not complete during my lifetime. Is there an algorithm which can make this job less time-consuming? Can anyone help me?

m_goldberg
  • 107,779
  • 16
  • 103
  • 257
wuchang
  • 151
  • 2
  • 4
    You may be able to approach this using Nearest. – DavidC Oct 25 '13 at 09:34
  • 5
    Just to clarify - is this about math/algorithms in general or specifically about the software Mathematica ? – Yves Klett Oct 25 '13 at 09:42
  • 1
    If this is about Mathematica then the answer is Nearest. If it is about algorithms and data structures, then I'd say it's off topic here and there are answers on StackOverflow here. – Szabolcs Oct 25 '13 at 16:26
  • 1
    To repeat what others have stated, you'll want to use Nearest[<reference set>]. Depending on specifics of locations, you may need to make adjustments to account for the fact that (long,lat) is not a Euclidean grid and moreover there is a singularity (crossover) for longitude. – Daniel Lichtblau Oct 25 '13 at 16:42

1 Answers1

5

Edit:

After reading about geodetic conversions, I decided to do a major rewrite. Earlier versions can be found by clicking on the "edited…" link. No claims are made about speed.

My intuitions about Geodesy are rudimentary, so I relied on ideas encountered at Latitude and Stack Exchange. I also

benefited from advice given by @Rahul Narain. Kuba also pointed me to an efficiency shortcut that Belisarius had recently used. 

(*Generate a random longitude in decimal degrees *)
rx:=RandomReal[{106.1000000000,106.2000000000},WorkingPrecision->10]

(*Generate a random latitude in decimal degrees *)
ry:=RandomReal[{41.4000000000,41.5000000000},WorkingPrecision->10]

(*radius of earth in km *)
r=6371;

(* 15 city points and 5 landmarks in Cartesian (XYZ) format *)
citypoints={r Cos[#2 Degree] Cos[# Degree],r  Cos[#2 Degree]Sin[# Degree],r Sin[#2 Degree]}&@@@Array[{rx,ry}&,15];
landmarks={r Cos[#2 Degree] Cos[# Degree],r  Cos[#2 Degree]Sin[# Degree],r Sin[#2 Degree]}&@@@Array[{rx,ry}&,5];

(* precomputed function for landmarks, to be used in Nearest *)
near=Nearest[landmarks];

(* each city point and its closest landmark *)
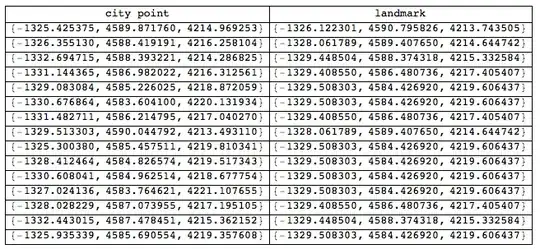
Grid[Prepend[{#,Nearest[landmarks,#][[1]]}&/@citypoints,{"city point","landmark"}],Dividers-> All]

table

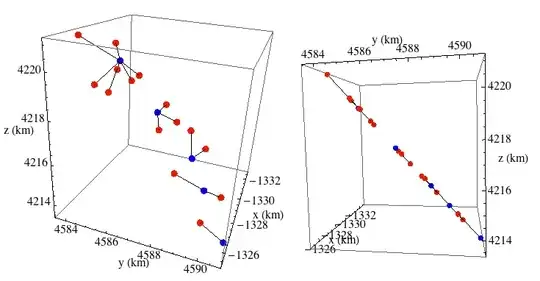
Plot the city points and landmarks. The origin is the center of the earth. x, y, z given in km. The picture in the right pane shows that the points appear to lie on a plane. Of course, we know they lie on a sphere (or ellipsoid), but the curvature of the earth is imperceptible at this scale and point of view. (Remember: all the points lie in a single city.)

(* city points in red, landmarks in blue.  Lines connect each city point to the closest  
landmark *)
Graphics3D[{Red,PointSize[.03], Point@citypoints,Blue,Point@landmarks,
Black,Line[{#,Nearest[landmarks,#][[1]]}&/@citypoints]},AxesLabel->{"x","y","z"},BoxRatios->{1,-1,-1},Axes-> True,ViewPoint->{2,.5,.5}]

enter image description here

Community
  • 1
DavidC
  • 16,724
  • 1
  • 42
  • 94
  • 1
    It will definitelly be faster if you precalculate NearestFunction: near = Nearest[landmarks]; ({#, near[#]} & /@ citypoints). Belisarius showed this lately – Kuba Oct 25 '13 at 09:49
  • 2
    You'll have to use Nearest with GeoDistance as the distance metric, not Euclidean. This will slow things down tremendously! – rm -rf Oct 25 '13 at 10:44
  • Presuming the long/lat, minutes, and seconds are converted to a single decimal, why won't euclidean work? Besides, isn't this a one-off computation? – DavidC Oct 25 '13 at 11:34
  • We are talking about 10^9 points here. I don't think the most obvious approaches will be useful here ... – Dr. belisarius Oct 25 '13 at 12:30
  • 1
    @DavidCarraher Because 1 minute E from (0,0) is not the same distance as 1 minute N from (0,0). This difference only gets worse the closer you get to the poles. GeoDistance will tell you that, whereas EuclideanDistance will consider them both equally distant. – rm -rf Oct 25 '13 at 15:37
  • 1
    Since the points represent "some places in a city" and so are likely to be quite close together relative to the size of the Earth, it might be enough to scale the longitudes by $\cos\phi_m$, where $\phi_m$ is the mean latitude, and then continue to use Euclidean distances, no? https://en.wikipedia.org/wiki/Geographical_distance#Spherical_Earth_projected_to_a_plane –  Oct 25 '13 at 17:14
  • Thanks rm-rf. I'll look into this more closely – DavidC Oct 25 '13 at 20:04
  • @Rahul. Yes, good advice. (Although I used different conversion formulas from decimal degrees to XYZ). Fortunately, Nearest can also handle distances in 3-space. – DavidC Oct 27 '13 at 13:51
  • This is a nice approach, but your conversion formulas are incorrect, as you can see by the fact that ParametricPlot3D[{r Cos[#2 Degree], r Cos[# Degree], r Sin[#]} & @@ {lon, lat}, {lon, -180, 180}, {lat, -90, 90}] is not a sphere. The formulas should be {r Cos[#1 Degree] Cos[#2 Degree], r Cos[#1 Degree] Sin[#2 Degree], r Sin[#1 Degree]} & instead. Also you might want to use BoxRatios -> Automatic in the plot so that distances are shown without distortion. –  Oct 27 '13 at 17:47
  • @RahulNarain. Thanks. That was due to sloppiness as well as misunderstanding the full meaning of the conversion formula. I did test the current formula using your criterion and it did produce a sphere, so I'm fairly certain that it now works. – DavidC Oct 27 '13 at 20:03