Change all Options of Plot Dynamically

Question

I am trying to make a series of changes in the appearance of the Plot of some function. I am trying to use Manipulate for my experiments. I tried to change the following code

Manipulate[ Plot[Sin[x], {x, 0, Pi}], {p, HoldForm /@ Options[Plot]}, {q, InputField}]

so that when, for example, p is AxesOrigin ->Automatic and q is changed to {-3,5} then the plot will be updated with Axes Origin at {-3,5}. Similar if p is taken AxesLabeL->None and p is changed to "A label" then the last plot will refreshed showing the label "A label" at the top(without affecting any changes already made in other options like AxesOrigin above).

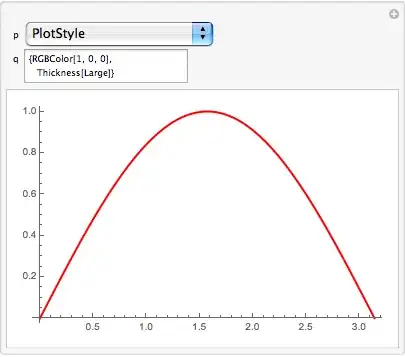
maybe this can get you started? Manipulate[With[{p1=p[[1,1]]},Plot[Sin[x],{x,0,Pi},p1-> q]], {{p,{PlotLabel-> None}, "Options"},Thread[{Options[Plot]}]},{{q,Null,"Value"},InputField}] — chuy, Nov 05 '13 at 19:16

C. E. · Answer 1 · 2013-11-09T09:35:45.207

5

Here's a different take on how to present the options, using SlideView rather than drop down, which is pretty nice.

I'm sorry for the fast animation, I had to drop a lot of frames to make its size decent.

{names, symbols, values} = 
  Transpose[Options[Plot] /. (Rule[x_, y_] | RuleDelayed[x_, y_]) :> {x, Unique[x], y}];
tables = 
   Partition[MapThread[Function[{name, symbol}, {
      Pane[name, 150], 
      InputField[Dynamic[symbol]]
   }], {names, symbols}], 10];
MapThread[Set, {symbols, values}];
Panel[
 Column[{
   Dynamic@
    Panel[Pane[
      Plot[Sin[x], {x, 0, 2 Pi}, 
       Evaluate[MapThread[Rule[#, #2] &, {names, symbols}]]], 
      BaseStyle -> {Background -> White}]],
   SlideView[
    TableForm /@ tables
    ]
   }]
 ]

animation

edited Nov 09 '13 at 09:35

answered Nov 07 '13 at 20:43

C. E.

70,533
6
140
264

gifsicle -O3 --colors 256 original.gif > smaller.gif brings it down from 1.8M to 784K – ssch Nov 07 '13 at 22:59
@ssch Nice, I'll remember that. Exported it from MMA this time. – C. E. Nov 08 '13 at 07:11

Michael E2 · Answer 2 · 2013-11-05T23:45:33.033

Here's way along the lines in the OP:

Manipulate[
 With[{opts = Sequence @@ opts},
  Plot[Sin[x], {x, 0, Pi}, opts]], {p, 
  PopupMenu[Dynamic[p, (q = opts[[#, -1]]; p = #) &],
    Thread[Range@Length@# -> #] &[First /@ Options[Plot]]] &},
 {{q, Null},
  InputField[
    Dynamic[q, (opts = ReplacePart[opts, {p, -1} -> #]; q = #) &]] &},
 {opts, None},
 TrackedSymbols :> {opts}, Initialization :> (opts = Options[Plot])

Mathematica graphics

kornaros · Answer 3 · 2013-11-05T20:46:51.730

I don't know if the following code will satisfies you. Of course one could change the code to add more controls like changing 0 and 2Pi corners e.t.c.

f[p_, pt : {___}] := Plot[p[x], {x, 0, 2 Pi}, pt]

 Manipulate[
 If[q =!= Null, PrependTo[r, p[[1, 1]] -> q]]; {p[[1, 1]] -> q, 
  f[Sin, r]}, {p, HoldForm /@ Options[Plot]}, {q, 
  InputField}, {{r, {Axes -> True}}, None}, TrackedSymbols -> {q}]

or similarly,

  Manipulate[If[q =!= Null, PrependTo[r, p[[1, 1]] -> q]]; 
 r = DeleteDuplicates[r, #1[[1]] == #2[[1]] &]; 
 Column@{r, p[[1, 1]] -> q, f[Sin, r]}, {p, 
  HoldForm /@ Options[Plot]}, {q, InputField}, {{r, {Axes -> True}}, 
  None}, TrackedSymbols -> {q}]

chuy · Answer 4 · 2013-11-05T20:27:32.340

Disclaimer -> this is quick and dirty (emphasis on dirty) first attempt:

Manipulate[
 plot[Sin[x],{x,0,Pi},Sequence@@{s,p[[1,1]]-> q}],
 {{p,{PlotLabel-> None}, "Options"},
 Thread[{Options[Plot]}]},
 {{q,Null, "Value"},InputField}, 
 {{s,{}},Block[{s2},Button["Save State", s2=Append[s,p[[1,1]]-> q];DeleteDuplicates[s2];s=s2]]&}, 
 Initialization:> 
  {plot[func_,{x_,xmin_,xmax_},opts:OptionsPattern[]]:= Plot[func,{x,xmin,xmax}, opts]}]

This (as badly written) has the limitations that you can pink box it with bad values for options. In order to "save a state" hit the button. Further changes should respect these previous ones.

Change all Options of Plot Dynamically

4 Answers4

Linked