Generating a graph where vertices correspond to points in an integer lattice and edges connect points less than a threshold distance apart

Question

I'd like to automatically generate a graph where vertices correspond to (and have the coordinates of) points in an $A \times B$ integer lattice, and a graph is generated by connected vertices within a real-valued cutoff distance $r$. Is there a (relatively) automated manner of doing this in Mathematica v9? How can we display this graph properly, respecting the vertex coordinates?

@belisarius That was a foolish mistake. I meant that the rules for connecting vertices should be the same as in a random geometric graph (connect vertices if the distance between them is $\leq r$). — user10456, Nov 08 '13 at 13:45

score 4 · Accepted Answer · edited Apr 13 '17 at 12:55

4

Make an integer lattice:

pts = Tuples[Range[10], 2]; (* maybe you want Tuples[{A,B}] *)

Find pairwise distances:

distances = 
  With[{tr = N@Transpose[pts]}, 
   Function[point, Sqrt[Total[(point - tr)^2]]] /@ pts];

Construct the graph:

threshold = 2;
SimpleGraph[AdjacencyGraph@UnitStep[threshold - distances], VertexCoordinates -> pts]

SimpleGraph is used to get rid of self loops.

edited Apr 13 '17 at 12:55

Community

1

answered Nov 08 '13 at 14:07

Szabolcs

234,956
30
623
1,263

Works perfectly. – user10456 Nov 08 '13 at 14:12

score 2 · Answer 2 · answered Nov 08 '13 at 14:22

2

By using Graph primitives.

g = GridGraph[{8, 9}];
vc = PropertyValue[{g, #}, VertexCoordinates] & /@ VertexList[g];
g1 = EdgeDelete[g, EdgeList[g]];
g2 = Fold[SetProperty[{#1, #2[[1]]}, VertexCoordinates -> #2[[2]]] &, 
                                                               g1, Transpose[{VertexList[g], vc}]]
cutoff = N@Sqrt[2];
f = Nearest[vc -> Automatic];
allEdgeSet = f[#, {Infinity, cutoff}] & /@ vc;
formattedEdges = Thread[UndirectedEdge[#[[2 ;;]], #[[1]]]] & /@ allEdgeSet;
randomEdges = DeleteDuplicates[Sort /@ Flatten[RandomSample[#, 2] & /@ formattedEdges]];
EdgeAdd[g2, randomEdges]

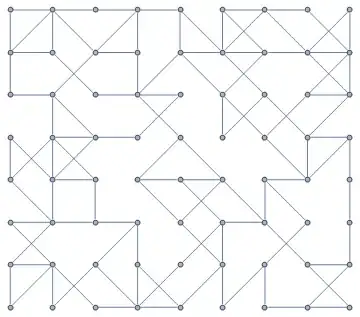
Mathematica graphics

answered Nov 08 '13 at 14:22

Dr. belisarius

115,881
13
203
453

What version of Mathematica are you using? For some reason, copy pasting this code, and using a fresh kernel, GridGraph is colored red and doesn't seem to work? – user10456 Nov 08 '13 at 14:25
@user10456 Mathematica v9. GridGraph was introduced in version 8 – Dr. belisarius Nov 08 '13 at 14:43
I owe you an apology, I left in a line asking the Combinatorica package to load. Removing it fixed the problem. – user10456 Nov 08 '13 at 14:44
@user10456 Yep, that's a common problem. "Combinatorica clashes" :) – Dr. belisarius Nov 08 '13 at 14:45

score 2 · Answer 3 · edited Nov 08 '13 at 17:47

General solution

I propose a general multidimensional solution with possibility to set periodic boundary conditions (I use a similar function in my own problem).

lattice[L_List, r_: 1] := 
 With[{d = Length[L], LL = Reverse@FoldList[Times, 1, Reverse@Abs@L][[1 ;; -2]]},
  With[{δ = Pick[#, UnitStep[# - 1] UnitStep[r^2 - #] &@Total[#^2, {2}], 1] &@
    Tuples[Range[-#, #] &@Ceiling[r], d]},
   Module[{Id = Join @@ Table[Transpose[{#, # + δ[[i]]}, {2, 3, 1}], {i, Length[δ]}] &@
     Transpose@Tuples[Range /@ Abs[L]] - 1},
    Do[If[L[[i]] > 0, 
      Id = Pick[Id, UnitStep[#] UnitStep[L[[i]] - 1 - #] &@Id[[All, 2, i]], 1],
      Id[[All, All, i]] = Mod[Id[[All, All, i]], -L[[i]]]], {i, d}];
    SparseArray[1 + Id.LL -> ConstantArray[1, Length[Id]]]
   ]]]

It returns the adjacency matrix for lattice with dimensions L (e.g. {10,5}).

Examples

1D lattice with 10 vertices

AdjacencyGraph@lattice[{10}]

enter image description here

1D lattice with 10 vertices with periodic boundary conditions (denoted by negative lengths)

AdjacencyGraph@lattice[{-10}]

enter image description here

1D lattice with 10 vertices with periodic boundary conditions and r = 2 (default value is 1)

enter image description here

$a\times b$ 2D lattice (OP's question)

a = 10;
b = 5;
r = 1.5;
AdjacencyGraph[lattice[{a, b}, r], 
 VertexCoordinates -> Join @@ Outer[List, Range[a], Range[b]]]

enter image description here

2D lattice with one periodic boundary

AdjacencyGraph@lattice[{10, -10}]

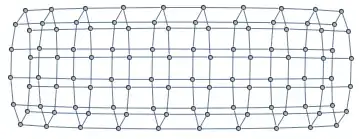
enter image description here

Tesseract

AdjacencyGraph@lattice[{2, 2, 2, 2}]

enter image description here

Notes

You can delete UnitStep[# - 1] to produce self-loops

enter image description here

It is fast for very big lattices ($1\,000\,000\times1\,000\,000$ adjacency matrix!)

lattice[{1000, 1000}]; // AbsoluteTiming

{2.718346, Null}

Szabolcs's approach with pairwise distances inapplicable for such lattices.

lattice uses packed array for big lattices. You can check it by On["Packing"].

Generating a graph where vertices correspond to points in an integer lattice and edges connect points less than a threshold distance apart

3 Answers3

General solution

Examples

Notes

Linked