Converting a Sierpinski tetrahedron to a Graph

Question

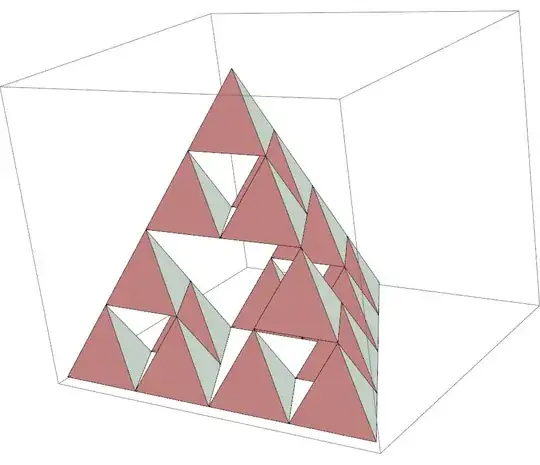
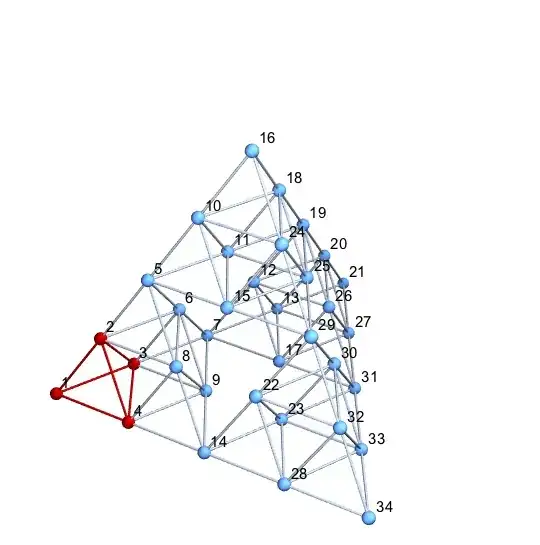
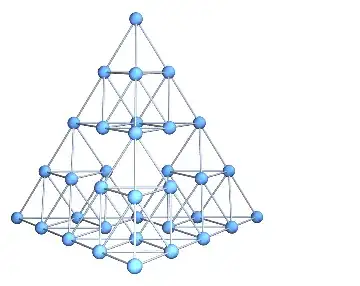
I need a representation of a 3D Sierpinski gasket as a graph to perform some simulations on. The 2D version is included in GraphData[], but the 3D one is nowhere to be found, so I was wondering if there is a way to convert Graphics3D objects to Graphs.

Say we have some geometry: (or even something as simple as Cuboid[]):

(*From Wiki =>*)
vect[1] = {0, 0, 0};
vect[2] = {1, 0, 0};
vect[3] = {0.5, 3^0.5/2, 0};
vect[4] = {0.5, 1/3*3^0.5/2, ((3^0.5/2)^2 - (1/3*3^0.5/2)^2)^0.5};
Tetron[{i_, j_, k_}] := 
  Tetrahedron[{vect[1] + {i, j, k}, vect[2] + {i, j, k}, 
    vect[3] + {i, j, k}, vect[4] + {i, j, k}}];
SiPyramid[0, {i_, j_, k_}] := {Tetron[{i, j, k}]};
SiPyramid[n_, {i_, j_, k_}] := 
  Module[{s = {}}, 
   Do[s = Union[s, 
      SiPyramid[n - 1, 2^(n - 1)*vect[u] + {i, j, k}]], {u, 4}]; s];

b = Graphics3D[SiPyramid[2, {1, 1, 1}]];
list = Cases[b, {x_?NumericQ, y_?NumericQ, z_?NumericQ}, Infinity];
Length[list];


lattice[L_List, r_: 1] := 
  With[{d = Length[L], 
    LL = Reverse@FoldList[Times, 1, Reverse@Abs@L][[1 ;; -2]]}, 
   With[{Δ = 
      Pick[#, UnitStep[# - 1] UnitStep[r^2 - #] &@Total[#^2, {2}], 
         1] &@Tuples[Range[-#, #] &@Ceiling[r], d]}, 
    Module[{Id = 
       Join @@ Table[
            Transpose[{#, # + Δ[[i]]}, {2, 3, 1}], {i, 
             Length[Δ]}] &@Transpose@Tuples[Range /@ Abs[L]] - 
        1}, Do[If[L[[i]] > 0, 
       Id = Pick[Id, 
         UnitStep[#] UnitStep[L[[i]] - 1 - #] &@Id[[All, 2, i]], 1], 
       Id[[All, All, i]] = Mod[Id[[All, All, i]], -L[[i]]]], {i, d}];
     SparseArray[1 + Id.LL -> ConstantArray[1, Length[Id]]]]]];

AdjacencyGraph[lattice[{8, 8}, 1], VertexCoordinates -> list]

This is how far I've gotten with this, but obviously some of the edge connections are wrong. Is there a more general way to perform this "conversion", or fix this method so that the links are right? Perhaps convert an .obj to a graph where vertices are nodes and edges are links?

Link to Lattice to Adjacency Matrix Source

UPDATE:

The figure can also be defined as

TetraVec[i_] := 2 IntegerDigits[3 i - 2, 2, 3] - 1;
tetrix[-1, p_: {0, 0, 0}] := Polygon /@ Array[TetraVec[#] +
            p & /@ Delete[Range[4], #] &, 4];
tetrix[n_, p_: {0, 0, 0}] := 
  Array[tetrix[n - 1, p + TetraVec[#] 2^n] &, 4];

Answer 1

A natural and simple way to approach this problem, assuming that your SiPyramid function has been defined, is as follows:

g = SiPyramid[1, {1, 1, 1}];
vertices = Union[g /. Tetrahedron[{vv__}] -> vv];
edges = Flatten[g /. Tetrahedron[vv_] :> 
  UndirectedEdge @@@ Subsets[vv, {2}]];
Graph3D[vertices, edges, VertexCoordinates -> vertices]

Unfortunately, this doesn't work for levels 2 and up. The reason is that vertices that appear where two fundamental tetrahedra intersect appear twice and the two copies are generated by different procedures. The procedures are algebraically equivalent but yield slightly different results numerically. We can demonstrate this by counting the number of vertices at level two:

g = SiPyramid[2, {1, 1, 1}];
vertices = Union[g /. Tetrahedron[{vv__}] -> vv];
vertices // Length

(* Out: 36 *)

If we perform the Union with a less stringent SameTest, we find that there are actually only 34 vertices:

Union[vertices, SameTest -> (Norm[#1 - #2] < 0.001 &)] // Length

(* Out: 34 *)

What we need is a tool to merge equivalent vertices. This is a common geometrical problem when precise connectivity information is needed. A similar problem arises in this tiling problem and we can use the same solution:

Needs["HierarchicalClustering`"]
canonicalFunction[nonCanonicalValues_List] := Module[
      {heirarchy, MyClusters, segregate, cf, clusters, 
    canonicalValues},
      Quiet[heirarchy = Agglomerate[N[nonCanonicalValues],
              DistanceFunction -> EuclideanDistance,
              Linkage -> "Average"]];
      segregate[Cluster[cl1_, cl2_, d_, _, _], tol_] :=   
    MyClusters[cl1, cl2] /; d > tol;
      segregate[mine_MyClusters, tol_] := 
    segregate[#, tol] & /@ mine;
      segregate[x_, _] := x;
      cf[cl_Cluster] := ClusterFlatten[cl];
      cf[x_] := {x};
      clusters = cf /@ 
     List @@ Flatten[FixedPoint[segregate[#, 10^(-12)] &,
                        MyClusters[heirarchy]]];
      canonicalValues = Chop[First /@ clusters];
      toCanonical[x_] := First[Nearest[canonicalValues][x]];
      toCanonical];

This canonicalFunction accepts a list of points and returns a function that transforms each of these individual points into a canonical representative. For example, given a tolerance of $0.1$, the list

{1,1.05,2,1.99,3,0.99}

could be transformed into

{1,1,2,2,3,1}

We can use it in your problem like so:

g = SiPyramid[4, {1, 1, 1}];
vertices = Union[g /. Tetrahedron[{vv__}] -> vv];
edges = Flatten[g /. Tetrahedron[vv_] :> 
  UndirectedEdge @@@ Subsets[vv, {2}]];

(* Generate the canonicalFunction *)
toCan = canonicalFunction[vertices];

(* Apply the canonicalFunction to merge vertices *)
vertices = Union[toCan /@ vertices];
edges = Map[toCan, edges, {2}];

Graph3D[vertices, edges, VertexCoordinates -> vertices]

One quick check is to generate the Graph3D without the VertexCoordinates option. In my experience, once you're missing some connectivity, the graph quickly flies apart. Using this technique, though, the topology looks correct:

Graph3D[vertices, edges]

Note that we've leveraged the fact that any expression can be a vertex. If you prefer a graph with integer indices, it is a simple matter to generate it. Here is the process for level 2.

g = SiPyramid[2, {1, 1, 1}];
vertices = Union[g /. Tetrahedron[{vv__}] -> vv];
edges = Flatten[
   g /. Tetrahedron[vv_] :> UndirectedEdge @@@ Subsets[vv, {2}]];

toCan = canonicalFunction[vertices];
vertices = Union[toCan /@ vertices];
edges = Map[toCan, edges, {2}];

(* Save the coordinates *)
vertexCoordinates = vertices;

(* Rename *)
globalCnt = 0;
newName[x_] := newName[x] = ++globalCnt;
vertices = newName /@ vertices;
edges = Map[newName, edges, {2}];

(* Draw with names *)
HighlightGraph[Graph3D[vertices, edges, VertexLabels -> "Name",
  VertexCoordinates -> vertexCoordinates],
Flatten[{1, 2, 3, 4,
  UndirectedEdge @@@ Subsets[{1, 2, 3, 4}, {2}]}]]

I suppose we could really illustrate the Graphiness of this object by illustrating a Hamiltonian path. Here it is at level 2. It's pretty easy to do with level 3 or 4 as well, but the exported animation is too large to upload to StackExchange.

{pathEdges} = FindHamiltonianCycle[g];
pathVertices = Prepend[Last /@ pathEdges, 1];
pics = Table[
   HighlightGraph[g, Join[pathVertices[[;; k]], pathEdges[[;; k]]]],
   {k, 1, Length[pathEdges]}];
Export["anim.gif", pics, "DisplayDurations" -> Append[
   Table[0.1, {Length[pathEdges] - 1}], 5],
 ImageSize -> 500]

Answer 2

There may be a simpler way to do this, but this function works for any object composed of Tetrahedron objects. I also made it work for MeshRegion objects of dimension 3. Expanding this to work with Polygon, Line, and Point objects should be straightforward.

tetGraph[tet3D_] := 
 With[{list = Cases[tet3D, Tetrahedron[a__] :> a]~Flatten~1},
  Graph[Range@Length@list, 
   Cases[tet3D, 
      Tetrahedron[a__] :> 
       UndirectedEdge @@@ (a[[#]] & /@ {{1, 2}, {1, 3}, {1, 4}, {2, 
            3}, {2, 4}, {3, 4}}), Infinity] /. 
     Thread[list -> Range@Length@list] // Flatten//DeleteDuplicatesBy[Sort],
   VertexCoordinates -> list]
  ]

; tetGraph[mesh_MeshRegion]:= tetGraph@MeshPrimitives[mesh,3]

tetGraph /@ {SiPyramid[2, {1, 1, 1}], SiPyramid[3, {1, 1, 1}], 
  SiPyramid[4, {1, 1, 1}]}

SeedRandom[42];
DelaunayMesh[RandomReal[{-5, 5}, {20, 3}]]
%  // tetGraph

Answer 3

Here's my take. The idea is similar to Mark's, except that I use ClusteringComponents[] to identify duplicate vertices, and VertexContract[] to merge those vertices together:

tetpts = N[PolyhedronData["Tetrahedron", "VertexCoordinates"], 20];
tet = Tetrahedron[tetpts];
tr = TranslationTransform /@ (tetpts/2);
makeEdge = Function @@ {MeshCells[BoundaryDiscretizeRegion[tet], 1] /. 
                        Line[l_] :> UndirectedEdge @@ Map[Slot, l]};

With[{n = 4},
     tx = Flatten[Nest[# /. Tetrahedron[pts_] :> Map[Tetrahedron[#[pts/2]] &, tr] &,
                       tet, n]];
     vc = Flatten[First /@ tx, 1]; idx = Range[4^(n + 1)];
     gt = Graph3D[idx, Flatten[makeEdge @@@ Partition[idx, 4]], VertexCoordinates -> vc];
     cl = ClusteringComponents[vc, 2 (4^n + 1), 1, Method -> "KMeans"];
     gt = Fold[VertexContract, gt, Cases[GatherBy[idx, cl[[#]] &], {_, _}]];
     gt = Graph3D[VertexList[gt], EdgeList[gt],
                  VertexCoordinates -> vc[[VertexList[gt]]], VertexSize -> Small]]

Answer 4

Altho this is a modification of my previous answer, I decided to post this separately, because the strategy for removing the duplicate points (a problem also touched upon by Mark) is different. This leverages the functionality of MeshRegion[], which apparently has the remarkable ability to detect and remove duplicate points. The code is now surprisingly compact and efficient:

tetpts = N[PolyhedronData["Tetrahedron", "VertexCoordinates"], 20];
tet = Tetrahedron[tetpts];
tr = TranslationTransform /@ (tetpts/2);

With[{n = 6}, (* ! *)
     tp = Flatten[Cases[Nest[# /. Tetrahedron[pts_] :> Map[Tetrahedron[#[pts/2]] &, tr] &,
                             tet, n], Tetrahedron[pts_] :> pts, ∞], 1];
     tm = MeshRegion[tp, Tetrahedron /@ Partition[Range[4^(n + 1)], 4]];
     Graph3D[Range[MeshCellCount[tm, 0]], UndirectedEdge @@@ (First /@ MeshCells[tm, 1]), 
             EdgeShapeFunction -> "Line", VertexCoordinates -> MeshCoordinates[tm]]]

---

Here is another minimal implementation (note that the resulting tetrahedron is scaled differently from the previous one):

tet = {{0, 0, 0}, {1, 0, 0}, {0, 1, 0}, {0, 0, 1}};
ts = tet/2; tr = {{1, 0, 0}, {1/2, Sqrt[3]/2, 0}, {1/2, 1/(2 Sqrt[3]), Sqrt[2/3]}};
With[{n = 6},
     tm = MeshRegion[Flatten[Nest[# /. mat_?MatrixQ :>
                                   (TranslationTransform[#][mat/2] & /@ ts) &, tet, n], n],
                     Tetrahedron[Partition[Range[4^(n + 1)], 4]]];
     Graph3D[Range[MeshCellCount[tm, 0]], 
             UndirectedEdge @@@ (First /@ MeshCells[tm, 1]), 
             EdgeShapeFunction -> "Line", VertexCoordinates -> MeshCoordinates[tm].tr]]

Answer 5

Update: Using MeshCells and Meshcoordinates with SierpinskiMesh (Thanks: @halmir):

sm = SierpinskiMesh[2, 3];
vertices = Range[MeshCellCount[sm, 0]];
edges = UndirectedEdge @@@ MeshCells[sm, 1][[All, 1]];
vcoords = MeshCoordinates[sm];

Graph3D[vertices, edges, VertexCoordinates -> vcoords, 
   VertexStyle -> Red,  VertexSize -> Medium, EdgeShapeFunction -> (Tube[#,.01] &)]

Original post:

sm = SierpinskiMesh[2, 3, 
  MeshCellShapeFunction -> {1 -> (Tube[#1, .01] &), 0->({Red,Sphere[#,.02]}&)},
  MeshCellStyle -> {{3, All}->Opacity[0],{2,All}->Opacity[0]}]

edges = Cases[Show[sm], Tube[x_, _] :> (UndirectedEdge @@@ x), Infinity][[1]];
vcoords = Show[sm][[1, 1]];
vertices = Range[Length@vcoords];

Graph3D[vertices, edges, VertexCoordinates -> vcoords]

Answer 6

IGraph/M has a convenience function for converting meshes to graphs while preserving vertex coordinates. It's as simple to use as

IGMeshGraph@SierpinskiMesh[2, 3]

The result is a weighted graph where graph edge weights correspond to mesh edge lengths. If you don't want weights, use

IGMeshGraph[SierpinskiMesh[2, 3], EdgeWeight -> None]

Answer 7

In version 12.1, one can now directly apply the new function MeshConnectivityGraph[] on SierpinskiMesh[]:

MeshConnectivityGraph[SierpinskiMesh[5, 3], PlotTheme -> "LargeNetworkDefault"]