Detecting a collision in n-body simulation with NDSolve

Question

Consider this three-body system:

g = 10; (* gravitational constant *)
m = {100, 1, 1}; (* masses *)
μ0 = g*m; (* gravitational parameters *)
r0 = {{0, 0, 0}, {1, 0, 0}, {-1.1, 0, 0}}; (* initial location vectors *)
v0 = {{0, 0, 0}, {0, 30, 0}, {0, -30.1, 0}}; (* initial velocity vectors *)

Differential equations for velocities and positions:

jmax = Length[m];
v = Evaluate[#] & /@ 
Table[ToExpression["v" <> ToString[j]], {j, jmax}];
r = Evaluate[#] & /@ 
Table[ToExpression["r" <> ToString[j]], {j, jmax}];
eqns[μ_List] := Flatten[Table[{
v[[j]]'[t] == 
 Sum[(-Normalize[r[[j]][t] - r[[i]][t]]*μ[[i]])/
  EuclideanDistance[r[[j]][t], r[[i]][t]]^2, {i, 
   Delete[Range[jmax], j]}],
r[[j]]'[t] == v[[j]][t],
v[[j]][0] == v0[[j]],
r[[j]][0] == r0[[j]]
}, {j, jmax}]]
fns = Flatten[Table[{v[[j]][t], r[[j]][t]}, {j, jmax}]]

The numerical integration stops when two bodies collide:

μ = μ0;
sol = NDSolve[eqns[μ], fns, {t, 0, 10}][[1]]
vel = (fns /. sol)[[1 ;; -2 ;; 2]];
pos = vel = (fns /. sol)[[2 ;; -1 ;; 2]];

NDSolve::ndsz: At t == 2.393483348087306`, step size is effectively zero; singularity or stiff system suspected. >>

The solution:

tmax = 2.393483348087306;
ParametricPlot3D[pos, {t, tmax - .1, tmax}, 
 PlotRange -> {All, All, {-.01, .01}}, ImageSize -> 800, 
 PlotPoints -> 500, MaxRecursion -> 15]

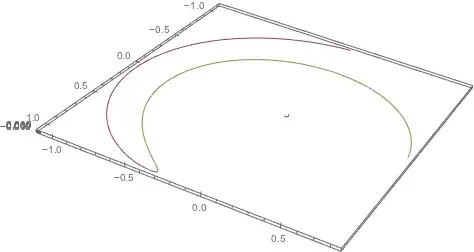
I would like to detect collisions and modify the computation so that the masses (and in effect, gravitational parameters) and velocities of the collided bodies change: one body's new mass becomes the sum of both masses and the new velocity becomes the sum of both velocities; the other body's new mass and velocity become zero.

I have tried to do it with WhenEvent:

μ = μ0;
sol = NDSolve[
Append[eqns[μ], 
WhenEvent[Length[$MessageList] > 0, Print[tmax = t];
 dist = 
  Table[EuclideanDistance[r[[j + 1]][t], r[[j]][t]], {j, 
    Length[r] - 1}];
 distDif = Table[Abs[dist[[n + 1]] - dist[[n]]], {n, Length[dist] - 1}];
 p = Position[distDif, Min[distDif]][[1, 1]];
 μ[[p]] += μ[[p + 1]]; μ[[p + 1]] = 0;
 v[[p]][t] += v[[p + 1]][t]; v[[p + 1]][t] = 0;
 "RestartIntegration"]], fns, {t, 0, 10}][[1]]
vel = (fns /. sol)[[1 ;; -2 ;; 2]];
pos = vel = (fns /. sol)[[2 ;; -1 ;; 2]];

However, this does not work. It seems that I do not catch the error properly, the program aborts before the message can be caught. How to catch this properly?

Answer 1

As mentioned in my comment I think it makes more sense if you try to detect the collision by investigating the current positions than examining $Messages. Here is how this can be done by introducing additional discrete variables for the masses:

g = 10;
m0 = {100, 1, 1};
r0 = {{0, 0, 0}, {1, 0, 0}, {-1.1, 0, 0}};
v0 = {{0, 0, 0}, {0, 30, 0}, {0, -30.1, 0}};

numbodies = Length[m0];

odesys = Table[{
    v[j]'[t] == UnitStep[m[j][t] - 0.01]*Sum[
       (-Normalize[r[j][t]-r[i][t]]*g*m[i][t])/EuclideanDistance[r[j][t], r[i][t]]^2,
       {i, Delete[Range[numbodies], j]}
       ],
    r[j]'[t] == v[j][t],
    v[j][0] == v0[[j]],
    r[j][0] == r0[[j]]
    },
   {j, numbodies}
   ];

initialmasses = Table[m[k][0] == m0[[k]], {k, numbodies}];

whenevnt = 
  With[{rmin = 
     Min[EuclideanDistance @@@ 
       Subsets[r[#][t] & /@ Range[numbodies], {2}]], 
    numbodies = numbodies},
   WhenEvent[rmin < 0.0001,
    pids = 
     SortBy[Subsets[Range[numbodies], {2}], 
       EuclideanDistance[r[#[[1]]][t], r[#[[2]]][t]] &][[1]];
    Print["collision at t=", t, " bodies:", pids];
    {m[pids[[1]]][t], v[pids[[1]]][t], m[pids[[2]]][t], 
      v[pids[[2]]][t]} -> {
      Total[
       m[#][t] & /@ pids], (m[#][t] & /@ pids).(v[#][t] & /@ pids)/
       Total[m[#][t] & /@ pids],
      0, {0, 0, 0}
      }
    ]
   ];

depvars = Flatten[Table[{v[j], r[j]}, {j, numbodies}]];

sol = NDSolve[
    Flatten[{odesys, initialmasses, whenevnt}],
    depvars, {t, 0, 5}, 
    DiscreteVariables -> Table[m[k], {k, numbodies}]
    ][[1]];

vel = Array[v, {3}] /. sol;
pos = Array[r, {3}] /. sol;
tmax = (Head[r[1][t] /. sol]@"Domain")[[1, 2]]

Animate[
 Show[
  ParametricPlot3D[Evaluate[#@tau & /@ pos], {tau, t - 0.1, t},
   PlotRange -> {3*{-1, 1}, 3*{-1, 1}, {-.01, .01}},
   ImageSize -> 800, PlotPoints -> 500, MaxRecursion -> 15, 
   Boxed -> False, Axes -> False,
   Background -> Black
   ],
  Graphics3D[{White, PointSize[Large], 
    Point[pos[[#]][t] & /@ Range[numbodies]]}]
  ],
 {t, 0.1, tmax},
 AnimationRepetitions -> 1, AnimationRate -> 0.5
 ]

Except for the mentioned change in the WhenEvent I have also made the following changes:

I am using expressions like r[1] instead of symbols like r1 as variables. It is one of the great things about NDSolve that this works and it of course makes the programmatic generation of variables much easier.

I have also changed the equations slightly: by setting one of the colliding masses to zero you want to make that effectively not interact anymore. That will fail because your equations implicitly were divided by m, which of course goes wrong when m=0. I have corrected that in a somewhat ad hoc way by using a UnitStep[m-eps], where you need to adjust eps so that it is smaller than any mass you want to use. Without that term, the zero-mass body would still see the forces of the others and that will make NDSolve stop because of "effectively zero stepsize" as before.

Of course for the general case you should add momentum, not velocities which I have also changed from your original code. For your particular case (nonrelativistic with equal masses colliding) it doesn't make a difference, though.

For the collision detection I have also used an arbitrary "small" number which in reality proably has to do something with the extent of the bodies and should be adjusted accordingly...

I also understand your units and the value of g to be arbitrary, and expect you are aware that you should use the gravitational constant (usually denoted G), not the free fall acceleration (usually g) in those equations...