What is the proper way to verify that two expressions are equal?

Question

First of all, it appears to me that

$$\left|\frac{1}{x} + x^2\right| = \frac{|1 + x^3|}{|x|}$$

is true.

I don't know why, but my attempt to verify it in Mathematica failed.

In[1]:= Abs[1/x + x^2] === Abs[1 + x^3]/Abs[x]
Out[1]= False

It's weird because Mathematica is unable to find a counterexample.

In[2]:= FindInstance[Abs[1/x + x^2] != Abs[1 + x^3]/Abs[x], x, Complexes]
Out[2]= {}

Answer 1

You are using SameQ which does a direct structural comparison rather than a mathematical one. Since the expressions are not exactly the same it returns False. Try Equal:

FullSimplify[Abs[1/x + x^2] == Abs[1 + x^3]/Abs[x]]

True

FullSimplify is needed for nontrivial comparisons; without it Mathematica will return the equality as given if it is not trivially equivalent.

You can also use ForAll and Resolve which I think is sometimes faster (no example at hand):

ForAll[x, x != 0, Abs[1/x + x^2] == Abs[1 + x^3]/Abs[x]] // Resolve

True

Answer 2

Answer

Given two symbolic expressions a and b in Mathematica, the way to check equivalence is:

True === FullSimplify[a == b]

Explanation

The FullSimplify function is a thorough symbolic restructuring command that will be most likely to reduce two equivalent symbolic expressions to True.

The === operator will call SameQ, which will return True if both operands are exactly equivalent without any manipulation and False otherwise.

The reason for adding the True === can be seen with an example.

a = d/2;
b = 4c;
FullSimplify[a == b]

 8c == d

That's not what we want though, and if we put this output in an If statement it will not work correctly. Since we want the only possible outputs to be True or False, we write:

a = d/2;
b = 4c;
True === FullSimplify[a == b]

 False

Yay!

Answer 3

The methodologies for this problem are advanced if the problem is discussed with persons who pose knowledge and competences with complex analysis.

Both functions have the same number of singularities and the same points. In fact the singularity is at $z=x=0$.

The singularity is in both of the order one. So multiplying both with $z$ removes the singularity.

For both we have the same set of zeros.

Solve[1/x + x^2 == 0, x, Complexes]

(* $\left\{\{x\to -1\},\left\{x\to \sqrt[3]{-1}\right\},\left\{x\to -(-1)^{2/3}\right\}\right\}$ *)

Solve[(1 + x^3)/x == 0, x, Complexes]

(* $ \left\{\{x\to -1\},\left\{x\to \sqrt[3]{-1}\right\},\left\{x\to -(-1)^{2/3}\right\}\right\} $ *)

ComplexPlot3D[(1 + z^3)/z, {z, -2 - 2 I, 2 + 2 I}, 
 RegionFunction -> Function[{z}, Abs[z] <= 1]]

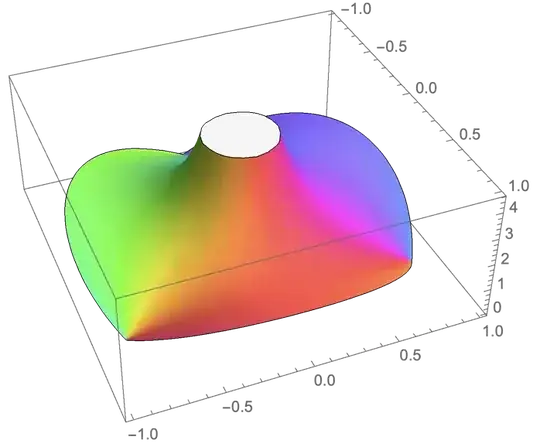
The limits are not zero at infinity. So it suffices to view the polynomial behavior up to the circle where the zeros are. The complex plot 3D clearly shows the three zero and the singularity.

ComplexPlot3D[1/z + z^2, {z, -2 - 2 I, 2 + 2 I}, 
 RegionFunction -> Function[{z}, Abs[z] <= 1]]

The difference between these two functions is a noise in the order of $MachinePrecision. So both functions are the very same over the complexes!

That is rigorous proof using complex analysis for the problem are these functions the same. Since both are only an operation different from each other called put on common nominator, here $x$.

Complex analysis is not only suitable, it is stringent needed. Because reals are not closed as the complexes are!

So mind that Mathematica follows a paradigm that all variables are in the complexes. This can be altered.

So the main problem from the task is dealing with the absolute function. This makes the comfort of the complexes pass always.

But we can treat the absolute value function by the very definition of it. The circle already shown is a brilliant restriction. Inside the absolute value has no effect, everything is positive. And it remains positive since there are only three zeros.

ComplexPlot3D[1/z + z^2, {z, -2 - 2 I, 2 + 2 I}, 
 RegionFunction -> Function[{z}, Abs[z] > 1]]

This complex 3D plot shows that the polynomial part dominates outside the circle. We have all diverges to plus infinity $+\infty$ as is expected for the polynomial $z^2$. This is a polynom with the zero $0$ of degree two. This is always positive and needs no action from the absolute function.

Same is the $z^-1$ with singularity at $z=0$ and going to $0$ from the positive side.

Adding two positive functions makes the resulting function not change sign.

So the absolute function is redundant over the complexes on the left hand side. $z$ and $z^3$ do change signs of course. The appear in the denominator and nominator of the right hand side function. The zeros are the very same on both this sign change is compensation. As is needed to be identical to the left hand side.

We get just in the denominator the factor $1+z^3$. That causes the zeros on the circle with radius $1$. Since the degree is three there are three of same. These have as explain no sign change in consequence. So an added constant results on the complexes in zeros!.

So this is the result: the absolute value taking is not in operation on both sides. We can discuss the two functions without it without change.

Both functions are the very same of the complexes. The reals are a subset of the complexes. By the laws of continuation follows the functions are identical over reals. This acknowledges that the functions under consideration are both unique up to an automorphism and whole functions. Which is true for polynomials and quotients of them.

But

Plot[1/x + x^2, {x, -2, 2}]

The zero is here clearly a point where the sign changes!. So we need the absolute function for this interval $\{-1,0\}$.

But as already shown over the complexes this does no weaken our result.

Plot[(1 + x^3)/x, {x, -1, 0}]

There is only a sign change imposed over this interval $\{-1,0\}$. This leads to a chase distinction for both over the same interval.

So a logical examination has to show all of these results to be considered valid!

FullSimplify 

states the answer correct, but does not have any details. It does show up that the weaker state has to be true, the identity without the absolute function.

So with which function are these contents generated or even detected in Mathematica. A treasure trove is the section Properties & Relation of the functions documentation.

We can use N or Expand. Both use conventions to show that the both functions are the same. The only result from this section for FullSimplify is that the Abs reduces the versatility of the relatives and properties very much.

The best help is the plot like this:

Plot[{1/x + x^2, Abs[1/x + x^2], (1 + x^3)/x, 
  Abs[(1 + x^3)/x]}, {x, -3, 3}] 

or

Reduce[1/x + x^2 < 0, x, Reals]

(* $-1<x<0$ *)

and

Reduce[(1 + x^3)/x < 0, x, Reals]

(* $-1<x<0$ *)

These result have to be identical.

SameQ[Reduce[1/x + x^2 < 0, x, Reals], 
 Reduce[(1 + x^3)/x < 0, x, Reals]]

(* True *)

We this we have that both functions are negative on the very same real interval $\{-1,0\}$. With FullSimplify or N we get that there are identical as from the consideration over the complexes. But our plot showed the absolute function is in action over the reals. There is no detailed or local insight with these methods.

We know $-1$ is one of the roots and $0$ is the singularity. So from the negative side the functions diverges to negative infinity $-\infty$. With the application of the absolute function this is changed and the resulting two functions diverges to $\infty$. No value is changes.

We know by experience that functions are identical if they have a common value and behave the very same on a real interval. This is only a reformulation of our results. The functions have a zero at $-1$ and diverge absolutely to $\infty$ is $0$ is approached.

Both function can be transformed into each other by Expand or Factor. Indeed

Factor[1/x + x^2]

(* $\frac{(x+1) \left(x^2-x+1\right)}{x}$ *)

This is another form of the two already in use. We worked around that with the Solve built-in.

So a more serious taken problem formulations would be:

$\frac{1}{x}+x^2=\frac{x^3+1}{x}=\frac{(x+1) \left(x^2-x+1\right)}{x}$

Then discuss the absolute function on this. That is mostly the question where, in which interval over the reals does it act on the given rational functions?

A closer look makes Expand obsolete. The pair of built-ins is Together and Apart. Both implement rewrite rules that a valid over the complexes with the local - global principles.

These are not logical functions. The Abs function is an obstacle for them. A logical part is the given

rationalFunctionQ[e_, vars_] := Module[{r = Together[e]}, Apply[And, PolynomialQ[#, vars] & /@ {Denominator[r], Numerator[r]}] ];

in the documentation page of Together. That is True for both functions of the posed problem. And this is another quality raising. This facts can be controlled if they are valid together with SameQ.

Over the complexes again the value of the steady derivative is important. The Abs functions destroys this attribute for function that have a zero and change sign. That is the deeper logic behind the problem.

The cuspoidal is unsteady in the zero $-1$ for the derivative. It is not necessary for logical statements about the identity but it is still present with that.

Together and Apart are inverse functions only partially but not in this problem. This can be read in the documentation of Together. So that there is an identity prior to the application of Abs. That is a general and fundamental mathematical truth!

Another good insight is

PiecewiseExpand[Abs[1/x + x^2], Reals]

(* $ \begin{cases} \frac{-x^3-1}{x} & x^2+\frac{1}{x}<0 \\ \frac{x^3+1}{x} & \text{True} \end{cases}$ *)

compared to

PiecewiseExpand[Abs[(1 + x^3)/x], Reals]

$\begin{cases} \frac{-x^3-1}{x} & x^2+\frac{1}{x}<0 \\ \frac{x^3+1}{x} & \text{True} \end{cases}$

This shows the reciprocity too.

PiecewiseExpand[Abs[1/x + x^2], Reals] == 
 PiecewiseExpand[Abs[(1 + x^3)/x], Reals]

(* True *)

To make it a logical statement from Mathematica without the theory from the complexes but still hiding Together and Apart. This makes no use of the conditions of when are two functions identical. It compares obsolete each point on the Reals.

The art is still then in the Assumption further than Reals to give insight, and make proper use of the local - global dilemmas of the other answers.