Different MeshStyle for different functions

Question

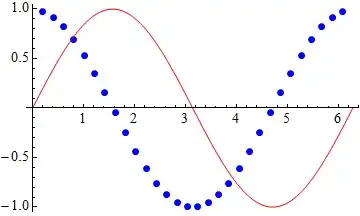
By using Plot command I want to get one curve in form of circles and other like a solid line.

Plot[{Cos[x], Sin[x]}, {x, 0, 2 Pi},
      PlotStyle -> {Opacity[0]}, Mesh -> 30, MeshStyle -> {PointSize[Large], Blue}]

enter image description here

score 7 · Accepted Answer · edited Apr 13 '17 at 12:55

Edit: Michael E2 notes that style None should be used instead of Opacity[0] because the former avoids drawing the line while the latter simply makes it invisible. I have changed all styles in the code below accordingly.

There may be a syntax to use a different Mesh for each curve (I cannot recall) but if not you can always fall back to plotting separately and combining with Show:

Show[
 Plot[Cos[x], {x, 0, 2 Pi}, PlotStyle -> None, Mesh -> 30, 
   MeshStyle -> Directive[PointSize[Large], Blue]],
 Plot[Sin[x], {x, 0, 2 Pi}, PlotStyle -> Red]
]

enter image description here

Two more ways to write the same thing:

Show[
 Plot[#[x], {x, 0, 2 Pi}, ##2] & @@@
  {{Cos, PlotStyle -> None, Mesh -> 30, 
    MeshStyle -> Directive[PointSize[Large], Blue]},
   {Sin, PlotStyle -> Red}}
]

Inner[
 Plot[#[x], {x, 0, 2 Pi}, #2] &,
 {Cos, Sin},
 {
  {PlotStyle -> None, Mesh -> 30, MeshStyle -> Directive[PointSize[Large], Blue]},
  PlotStyle -> Red
 },
 Show
]

It is nice to see how many questions that one has have been already asked and solved by other people! Mathematica syntax seems quite complex to me. I appreciate this website very much! — Vicent, Jul 01 '14 at 12:58

score 1 · Answer 2 · edited Apr 13 '17 at 12:55

1

[Works on V7-V10, Mac OSX.] Adapting my answer to the OP's other question, we can use PlotStyle to achieve the same effect with evenly spaced dots.

Plot[{Cos[x], Sin[x]},
 {x, 0, 2 Pi}, 
 PlotStyle -> {Directive[CapForm["Round"], Dashing[{0, 0.05}], Thickness[0.02]],
               Directive[]}]

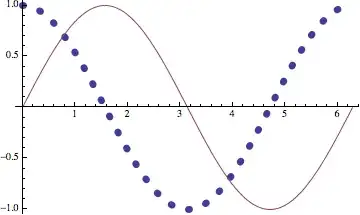
Mathematica graphics

Caveat: The CapForm["Round"] directive does not seem to be honored in Windows (at least with respect to Dashing in PlotStyle), according to a comment to my answer to the linked question.

Side notes: The setting PlotStyle -> {Opacity[0]} in the OP's example code produces a curve, a Line object in fact, that cannot be seen. The setting PlotStyle -> None causes Plot not to produce a Line object at all.

I've never been able to figure out how to apply different mesh specifications to different functions using one Plot. I do it in the way Mr. Wizard has shown.

edited Apr 13 '17 at 12:55

Community

1

answered Dec 26 '13 at 14:36

Michael E2

235,386
17
334
747

1

Unfortunately your caveat is true: this does not work in v7 under Windows, though CapForm["Round"] works elsewhere. – Mr.Wizard Dec 26 '13 at 14:39
1

@Mr.Wizard Oh, bother, as Pooh says. – Michael E2 Dec 26 '13 at 14:44
Nice tip regarding PlotStyle -> None. – Mr.Wizard Dec 26 '13 at 14:46
"Oh, bother" I say that a lot too. :^) – Mr.Wizard Dec 26 '13 at 14:46
1

This is a perfect method; it's a shame that this has not been fixed in recent versions for Windows. I wonder if the back end graphics engine somehow doesn't support this. Do you know which APIs are used on your platform? – Mr.Wizard Dec 26 '13 at 14:51
@Mr.Wizard I'm not sure I know what you're asking. Would OpenGL be an appropriate answer? See Apple's overview. – Michael E2 Dec 26 '13 at 15:49
I'm not sure what I'm asking either. :o) Graphics used to be rendered down to PostScript (pre-v6) but I don't know what the current graphics interface, engine, or API structure is. From past experience platform differences are often due to the system frameworks and APIs that are used. I wonder if there is a long-term bug (or stubborn incompatibility) in the Windows back end that this failure. – Mr.Wizard Dec 26 '13 at 17:25
@Mr.Wizard I know nothing relevant. What happens with other cap forms ("Square" vs. "Butt"). My default looks like "Square", but in Windows, CapForm["Round"] looked like "Butt". – Michael E2 Dec 26 '13 at 17:55
CapForm appears to have no effect on Dashing. – Mr.Wizard Dec 26 '13 at 23:16

score 0 · Answer 3 · edited Jun 16 '20 at 09:23

MeshFunctions

You can use # Boole[#2 == foo[#]] & as the MeshFunctions setting to have the mesh points only on the curve of the function foo. For example:

Plot[{Cos[x], Sin[x]}, {x, 0, 2 Pi}, PlotPoints -> 300, 
 PlotStyle -> {None, Red},
 MeshFunctions -> {# Boole[#2 == Cos[#]] &}, Mesh -> 30, 
 MeshStyle -> Directive[PointSize[Large], Blue]]

Plot[{Cos[x], Sin[x], Sin[x] + Cos[x]}, {x, 0, 2 Pi}, PlotPoints -> 300,
 PlotStyle -> {None, Red, Green},
 MeshFunctions -> {# Boole[#2 == Cos[#]] &}, 
 Mesh -> 30, MeshStyle -> Directive[PointSize[Large], Blue]]

Plot[{Cos[x], Sin[x], Sin[x] + Cos[x]}, {x, 0, 2 Pi}, PlotPoints -> 300,
 PlotStyle -> {Blue, Red, None},
 MeshFunctions -> {# Boole[ #2 == Sin[#] + Cos[#]] &}, 
 Mesh -> 30, MeshStyle -> Directive[PointSize[Large], Green]]

Post-processing

ClearAll[postProcess, prims]
prims[x_, msh_, j_] := RotateRight[{{PointSize[Large], Point[Intersection[x, msh]]}, 
 Line[x], Line[x]}, j - 1]
postProcess[j_] :=  Module[{i = 1}, # /.  Block[{msh}, {Point[x_] :> (msh = x; {}), 
 Line[x_] :> (prims[x, msh, j][[i++]])}]] &;
plot = Plot[{Cos[x], Sin[x], Sin[x] + Cos[x]}, {x, 0, 2 Pi}, Mesh -> 30,
 PlotStyle -> {Blue, Red, Green}];
postProcess[2]@plot

 postProcess[1]@plot

Different MeshStyle for different functions

3 Answers3

MeshFunctions

Post-processing

Linked