GridLines in LogPlot or LogLogPlot

Question

Suppose I have a plot like

LogLogPlot[2 x^5/3, {x,0.1,10}, GridLines->Automatic]

How can I achieve to get "custom" gridlines to reduce the number of horizontal lines?
I know how to do it with linear scaled plot.

Edit

For linear scale I do basicly:

myGrid[{xmin,xmax,xstep}, {ymin,ymax,ystep}]:=
GridLines->{{#&,/@Range[xmin,xmax,xstep},{#&/@Range[ymin,ymax,ystep])}

What's wrong with LogLogPlot[2 x^5/3, {x, 0.1, 10}, GridLines -> {{.2, .5, 1, 2, 5}, {.001, .01, .1, 1, 10, 100, 1000}}]? — Szabolcs, Apr 09 '12 at 15:36
What have you tried? Have you tried using your linear scaled plot techniques with LogLogPlot? — rcollyer, Apr 09 '12 at 15:37
Maybe you're asking how to customize one set of lines while preserving automatic spacing for the other? As in LogLogPlot[2 x^5/3, {x, 0.1, 10}, GridLines -> {Range[5], Automatic}] or the other way around... — Jens, Apr 09 '12 at 15:42
@Szabolcs: Yes, I know, that I can give the list explicitly. But I search for a way to only give the values in one "decade", which then applies for every decade. Something like gridlines[{1,2,5},{1,3,7}], which sets lines in each decade at these values. — Peter Breitfeld, Apr 09 '12 at 15:48
@Peter How do you do that with linear scale plots? Can you compare? — Szabolcs, Apr 09 '12 at 15:50
@Peter Are you looking for GridLines -> {Automatic, Flatten@Table[{1, 2, 5} 10^i, {i, -5, 5}]} or something similar? — Szabolcs, Apr 09 '12 at 15:58
@Szabolcs something similiar I even tried, but this gives more than three lines in one decade. I would like to have n lines, if the list has length 3. — Peter Breitfeld, Apr 09 '12 at 16:08

Peter Breitfeld · Answer 1 · 2012-04-10T13:05:50.527

After some fiddling around I came up with this function:

Clear[gitter]
gitter[xspec_, yspec_, logPlot_: False] :=

  Module[{min, max, d, xlines, ylines, i},
   xlines = ylines = None;
   Switch[xspec,
    Automatic, xlines = Automatic,
    {_?NumericQ, _?NumericQ, _?NumericQ},
    {min, max, d} = xspec;
    xlines = Range[min, max, d],
    {_?NumericQ, _?NumericQ, _List},
    {min, max, d} = xspec;
    If[logPlot == False,
     xlines = (Log10[#] &) /@ Flatten[Table[10^i*d, {i, min, max}]],
     xlines = Flatten@Table[10^i d, {i, min, max}]]
    ];
   Switch[yspec,
    Automatic, ylines = Automatic,
    {_?NumericQ, _?NumericQ, _?NumericQ},
    {min, max, d} = yspec;
    ylines = Range[min, max, d],
    {_?NumericQ, _?NumericQ, _List},
    {min, max, d} = yspec;
    If[logPlot == False,
     ylines = (Log10[#] &) /@ Flatten[Table[10^i*d, {i, min, max}]],
     ylines = Flatten@Table[10^i d, {i, min, max}]]];
   {xlines, ylines}];

It handles three cases:
(1) Linear scale: The parameters have the form {min, max, step}
(2) logarithmic scale in a normal Plot: The parameters have the form {min, max, istOfValues}
(3) LogPlot or LogLogPlot: as in (2) but the optional Parameter LogPlot has to be set to True.

Examples:

grid = gitter[{-1, 1, {1, 2, 5, 7}}, {-5, 5, {1, 2, 5, 7}}, True];
lp = LogLogPlot[2 x^5/3, {x, 0.1, 10}, GridLines -> grid, 
  PlotRangePadding -> 0, AspectRatio -> 1, 
  Ticks -> {Automatic, Table[10.^i, {i, -5, 5}]}]

gives:

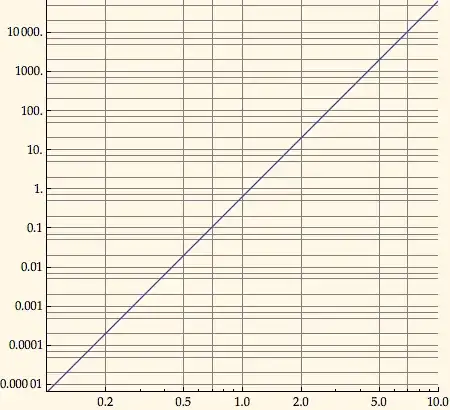
enter image description here

and

yticks = Tickmarken[0, 5, {1}, {2, 3, 5, 7}];
gitter = Gitter[{-2, 10, 1}, {0, 5, {1, 2, 3, 5, 7}}];
plot = Plot[Log10[2 E^x], {x, -2, 10}, Ticks -> {Automatic, yticks}, 
  GridLines -> gitter]

gives:
enter image description here

Tickmarken is a function, I use to make Ticks.

score 1 · Answer 2 · answered Apr 09 '12 at 17:08

As best I understand, this should do about what you want. You could of course make the {1,2,5} a parameter of the gridlines function.

gridlines[min_, max_] := 
 Block[{}, 
  Flatten[Outer[Times, {1, 2, 5}, 
    10^Range[Floor[Log10[min]], Ceiling[Log10[max]]]]]]

LogLogPlot[2 x^5/3, {x, 0.1, 10}, GridLines -> {gridlines, gridlines}]

enter image description here

GridLines in LogPlot or LogLogPlot

Edit

2 Answers2

Linked