Having known the fact that the evaluation of the integrals containing fractional parts often contains
errors, I wonder if the integral below possibly evaluates to $0.7$ or this is just a coincidence that
N[Integrate[Tan[x] - Floor[Tan[x]], {x, 0, Pi/2}], 16]
yields $0.6991518856432281$. How could I check if $0.7$ is or isn't the right answer?
We can get the result easily if we observe a simple fact, that such an integral can be evaluated symbolically:
Integrate[ Tan[x], {x, ArcTan[n], ArcTan[n + 1]}, Assumptions -> n ∈ Integers && n > 0]
- n (ArcTan[n + 1] - ArcTan[n])
-n (-ArcTan[n] + ArcTan[1 + n]) + 1/2 Log[1 + (1 + 2 n)/(1 + n^2)]
Now we can just sum the above series form n == 0 to infinity:
NSum[ -n (-ArcTan[n] + ArcTan[1 + n]) + 1/2 Log[1 + (1 + 2 n)/(1 + n^2)], {n, 0, ∞}]
0.69836
Edit
It appears that although indirectly, we can get the symbolic result as well.
We have to transform terms involving ArcTan to logarithms with the help of TrigToExpbefore calculating it with Sum (precedence is crucial) :
Sum[ -n (-ArcTan[n] + ArcTan[1 + n]) + 1/2 Log[1 + (1 + 2 n)/(1 + n^2)] // TrigToExp, {n, 0, ∞}] //
FullSimplify // TraditionalForm
This sum is expressed in terms of the Euler gamma function and first derivatives of the Riemann zeta function and although it doesn't seem to be real we can get the real part of it.
N[ Re[%], 40]
0.6983596795324668021124683422031034593401
We have had to take the real part of the sum since we've encountered an arbitrary Mathematica rule for calculation of logarithm function braches in the complex domain, see e.g. this post Why does Integrate declare a convergent integral divergent?
If you flip the area being calculated about the line $y=x$, you get that the following two integrals are equivalent:
Integrate[Tan[x] - Floor[Tan[x]], {x, 0, Pi/2}]
Integrate[ArcTan[Ceiling[y]] - ArcTan[y], {y, 0, Infinity}]
The second is equal to the limit of the difference of the integral and the sum, as n approaches Infinity:
int = Integrate[ArcTan[x], {x, 0, n}, Assumptions -> n > 0]
sum = Sum[ArcTan[k], {k, n}]
You can but you don't have to trust the Numerical Calculus package:
Needs["NumericalCalculus`"];
NLimit[sum - int, n -> Infinity]
(*
0.69836
*)
You don't have to, because the error of sum - int for a given n is less than Pi/2 - ArcTan[n]. So for 6 digits of accuracy, evaluate for n -> 10^6.
sum - int /. n -> 10^6 // N
(*
0.698359
*)
Some pictures to show the equivalence:
Plot[{Tan[x], Floor[Tan[x]]}, {x, 0, Pi/2}, Filling -> {1 -> {2}}]
Plot[{ArcTan[Ceiling[x]], ArcTan[x]}, {x, 0, 7}, Filling -> {1 -> {2}}]
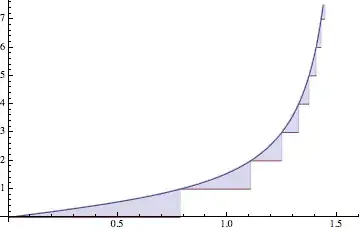
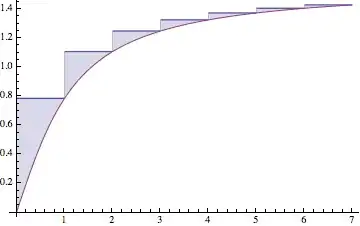
Below we can see that sum - int underestimates the integral and the error is actually less than (Pi/2 - ArcTan[n])/2, the factor of 1/2 following from the concavity of ArcTan. (The error consists of "concave triangles" that fit in the space above the last triangle and below $y=\pi/2$.)
Show@Table[
ParametricPlot[
{1 - t, t}.{{x - i + 1, ArcTan[i]}, {x - i + 1, ArcTan[x]}},
{x, i - 1, i}, {t, 0, 1},
Mesh -> None, PlotRange -> {Automatic, {0, Pi/2}}],
{i, 10}]
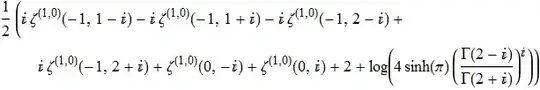
NSum[-n (-ArcTan[n] + ArcTan[1 + n]) + 1/2 Log[1 + (1 + 2 n)/(1 + n^2)], {n, 0, ∞}, AccuracyGoal -> 15, WorkingPrecision -> 30]which yields0.6983596795324668. – Artes Jan 19 '14 at 22:20Gammais a generalization ofFactorial, I wanted to update my answer here since I was sure there had to be a more elegant form but I've been busy recently, now I guess you don't expect any updates of my answer, do you? – Artes Feb 01 '14 at 20:48