I dont know how to do this automatically, to find bouded region given with those surfaces. I guess ou could take each three and check if there is a finite intersection and then combine the result.
Meanwhile you can plot it as I've suggested and as Nasser has shown to get an idea what to loog for:
ContourPlot3D[{z==x y, z==0, y==x^2, x==y^2}, {x, #, #2}, {y, #3, #4}, {z, #5, #6},
Mesh -> 1, ImageSize -> 500, BaseStyle -> 18, ViewPoint -> {5, 1, 2},
ContourStyle -> (Directive @@@ {{Red}, {Green}, {Blue, Opacity@.3}, {Yellow}}),
Lighting -> "Neutral", AxesLabel -> {"x", "y", "z"}
] & @@@ {{-2, 2, -2, 2, -2, 2}, {0, 1, 0, 1, -.1, 1.1}} // Row

Ok, now we know:
RegionPlot3D[And @@ {z <= x y, z >= 0, y > x^2, x > y^2},
{x, -.02, 1.1}, {y, -.02, 1.1}, {z, -.02, 1.02},
Mesh -> 50, ImageSize -> 500, PlotPoints -> 100, MaxRecursion -> 10,
PlotStyle -> None]
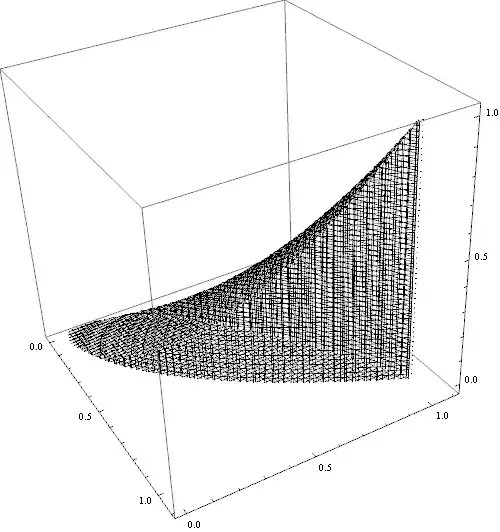
Hard to get that tip in {0,0,0} :/. Ok, copy and paste first part of former code:
NIntegrate[ Boole[And @@ {z <= x y, z >= 0, y > x^2, x > y^2}],
{x, -.02, 1.1}, {y, -.02, 1.1}, {z, -.02, 1.02}]
0.0833333



ContourPlot3D. – Kuba Jan 27 '14 at 15:03RegionPlot3D. – Szabolcs Jan 27 '14 at 16:01x^2+y^2=1is a sphere, whilex^2+y^2<=1is a sphere. – Kuba Jan 29 '14 at 12:52=doesn't indicate if he wants the region "inside" or "outside" (or left/right, above/below, etc.). To use your example, doesx^2 + y^2 =1imply the solid sphere with radius 1 or the entire space except that sphere? :) Since the OP seems to have accepted your answer, please edit the question to fit the best possible interpretation and I'll gladly add a reopen vote :) – rm -rf Jan 29 '14 at 18:21=doesn't but with: "I would like to integrate the region bounded by them." it is clear we are talking about finite volume :). It is not obvious such region exists but OP does not share this concern with me. And existance or finding those regions are separate questions. That's why I have nothing to edit :/. – Kuba Jan 29 '14 at 23:11