2

I have the following numbers

l={38, 38, 38, 38, 38, 38, 38, 38, 38, 38, 38, 37, 37, 37, 37, 37, 37,
37, 36, 36, 36, 36, 36, 36, 36, 36, 36, 36, 36, 36, 36, 36, 36, 36,
35, 34, 34, 34, 34, 34, 33, 33, 33, 33, 33, 32, 31, 29, 29, 29, 28,
28, 28, 28, 27, 26, 25, 23, 21, 21, 16, 15, 15, 15, 11, 10, 6, 5, 4,
4, 4, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0}

which look like an error function. I'd like to automatically find a fit for these numbers. I tried two different approaches

Fit[l, {Erf[x], 1}, x]

and

FindFit[l, a Erf[b x - c] + d, {a, b, c, d}, x]

Both produce completely off results. As I have a lot of data lists, I'd very much appreciate to automatically find the fits for these data.

Greg Hurst
  • 35,921
  • 1
  • 90
  • 136
Mockup Dungeon
  • 1,854
  • 12
  • 16
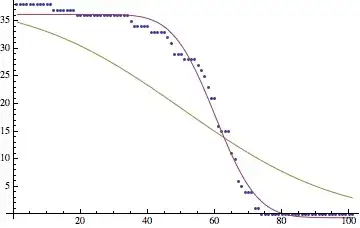
  • Here’s a possible approach: sol = FindFit[l, {a Erfc[b (z - c)], a > 10, 0 < b < 0.1, 30 < c < 60}, {a, b, c},z] which gives {a -> 18.1322, b -> 0.0740242, c -> 59.7275} then Show[Plot[a Erfc[b (z - c)] /. sol, {z, 0, 100}], ListLinePlot[l], PlotRange -> All]. – Stephen Luttrell Feb 11 '14 at 18:31
  • @Stephen Thanks. That works, but a lot of manual adjustment is required. I was hoping for something even more automatic. – Mockup Dungeon Feb 11 '14 at 18:57
  • In the documentation for FindFit it says "In the nonlinear case, it finds in general only a locally optimal fit.", which means that it helps to impose constraints on the parameter values as I did. I didn't play with any of the possible settings for the Method option of FindFit, so you might find a better approach hiding in there somewhere. – Stephen Luttrell Feb 11 '14 at 19:08
  • @Stephen OK, thanks for the help. – Mockup Dungeon Feb 11 '14 at 21:06
  • And if someone is downrating this question, then please enlighten me where I'm wrong that fitting such data appears not simple. It would be much appreciated. – Mockup Dungeon Feb 11 '14 at 21:16

2 Answers2

5

As Stephen Luttrell has been pointed in the comments, the problem is that FindFit is not guaranteed to find a globally optimal fit in the nonlinear case. This is a property it shares with the similarly named functions FindRoot and FindMinimum. However, instead of imposing constraints, I would recommend just giving the algorithm a better starting point from which to start the numerical search, and then it should be able to converge to the fit you want. (I guess the reason it works better with the ArcTan in RiemannZeta's answer is that Erf's derivatives drop so rapidly to zero that the algorithm can't find a useful gradient using the default initialization.)

In your given example, it's easy to pick a good initial guess just by eyeballing the numbers. Since you want to automate this for arbitrary data, though, here's an initialization strategy that should be well-conditioned for most sigmoid-shaped inputs. All it does is map $-1\le x\le1,-1\le y\le1$ in the graph of Erf to the length and the min-max range of the data.

f[x_] := a Erf[b x - c] + d;

a0 = If[First@l < Last@l, 1, -1] (Max@l - Min@l)/2;
b0 = 2/Length@l;
c0 = 1;
d0 = (Max@l + Min@l)/2;

fit = FindFit[l, f[x], {{a, a0}, {b, b0}, {c, c0}, {d, d0}}, x]

(* {a -> -18.4315, b -> 0.0721048, c -> 4.33237, d -> 17.823} *)

Show[
 ListPlot[l], 
 Plot[f[x] /. {a -> a0, b -> b0, c -> c0, d -> d0}, {x, 1, Length@l},
  PlotStyle -> ColorData[1][3]], 
 Plot[f[x] /. fit, {x, 1, Length@l}, PlotStyle -> ColorData[1][2]]]

enter image description here

The data is in blue, the initialization is in yellow, and the optimized fit is in red.

2

For what it's worth, replacing Erf with ArcTan gives a better result for this particular example.

sol = a ArcTan[b (x - c)] + d /. FindFit[l, a ArcTan[b (x - c)] + d, {a, b, c, d}, x]

(* 17.3813 - 13.6427 ArcTan[0.139271 (-60.7409 + x)] *)

Then we can plot

Show[
 ListLinePlot[l],
 Plot[sol, {x, 1, Length[l]}, PlotStyle -> ColorData[1][2]]
]

We can then take ArcTan to Erf

solErf = sol /. ArcTan[f_] :> π/2 Erf[f]

(* 17.3813 - 21.4298 Erf[0.139271 (-60.7409 + x)] *)

This gives an 'ok' fit in terms of Erf

Show[
 ListLinePlot[l],
 Plot[solErf, {x, 1, Length[l]}, PlotStyle -> ColorData[1][2]]
]

Greg Hurst
  • 35,921
  • 1
  • 90
  • 136
  • OK, thanks. I didn't expect the fit business to be rather complex. I'd thought finding a fit for such data would be more straight forward. Interesting to learn this lesson. As said, I'd like to have this automated for ~100 such datasets, so adjusting every time is somewhat tedious, although obviously necessary. – Mockup Dungeon Feb 11 '14 at 21:10