10

I have several large data sets which follow the following pattern: A position is measured, a force is applied until a new equilibrium is found.
I'd like to find a fit for the position, at least at the plateaus, and preferably of the inter lying section, which in this case approaches a line.
I tried fitting the data with Clip, and with Piecewise. 

nlm = NonlinearModelFit[v40s1000h,Piecewise[{{a, x < A}, {b, x > B}}], {a, b, A, B, c, d}, x]

This creates a decent fit only if I specify the values for A and B, but then I have to estimate those values for each data set manually. It also doesn't really work to just add NMinimize, or add the piecewise part for the middle bit.
Is There anything else I can try?

Setting the A to 200 and B to 250 works decently.

http://s000.tinyupload.com/?file_id=35616536027018518052 << file

Karsten7
  • 27,448
  • 5
  • 73
  • 134
Feyre
  • 8,597
  • 2
  • 27
  • 46
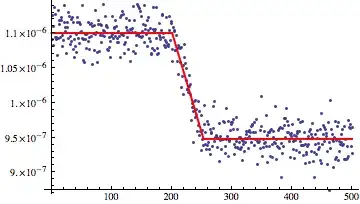
  • Could you post a link to the dataset v40s1000h. An idea would be to create the first few terms of a Fourier expansion and fit that within the domain of interest. – gpap Apr 10 '14 at 10:08
  • @Feyre I don't understand, you're saying that you need to manually specify A,B, but in your example you are fitting the parameters A,B. – sam84 Apr 10 '14 at 10:09
  • 1
    How about fitting a sigmoid? – Peltio Apr 10 '14 at 10:55
  • 2
    I think NonlinearModelFit works my minimizing some cost function (e.g. total squared error), but the cost function can't be evaluated if your piecewise function doesn't return a value for some values of x. Have you tried using something like {(a+b)/2,A<x<B} as a fallback? Alternatively, you could come up with your own cost function and just optimize that. – Niki Estner Apr 10 '14 at 11:06
  • well, these are guesses I made, and they fit, the images was made with those guesses, which does work, but I'd have to guess for each separate file. Fitting with just the parameters A and B yields just a single straight line, and it tries to fit them around ~13x.

    gpap, Peltio I haven't had too much maths yet, I know basic Fourier series and transforms, but that's it. Could you give more of an idea (or a link) on how to try this in Mathematica?

     – Feyre Apr 10 '14 at 11:10
  • File: http://s000.tinyupload.com/?file_id=35616536027018518052 – Feyre Apr 10 '14 at 11:11
  • @nikie
    The original was: Piecewise[{{a, x < A}, {c x + d, A < x < B}, {b, x > B}}], which yields a single straight line.     – Feyre Apr 10 '14 at 11:15
  • @Feyre, could you put that file up somewhere else? Some proxies (like the one I'm behind) evidently block tinyupload.com as a high risk site? It's only about a dozen kiB. – Pillsy Apr 10 '14 at 11:20

1 Answers1

15

As usual, it's a matter of choosing a better starting values for the parameters.

I started writing this answer before the data file was uploaded, so here's some synthetic data:

data = Table[
   Interpolation[{{0, 1.1*^-6}, {200, 1.1*^-6}, {250, 9.5*^-7}, {500, 
       9.5*^-7}}, x, InterpolationOrder -> 1] + 
    2*^-8 RandomVariate[NormalDistribution[]], {x, 0, 500}];
ListPlot[data]

enter image description here

As @nikie suggested in the comments, you should define your model to return something in the intermediate values. I'll use a linear transition because that seems to match your data.

f[x_] := Piecewise[{{a, x < xa}, {a + (b - a) (x - xa)/(xb - xa), xa <= x < xb}, {b, xb <= x}}]

Now we do the fit:

fit = NonlinearModelFit[data, f[x], {a, b, xa, xb}, x];
fit // Normal // InputForm
(* Piecewise[{{1., x < 1.}, {1.016964195743597*^-6, 1. <= x}}, 0] *)

No good. Why? The documentation for NonlinearModelFit says "give starting values when parameters are far from the default value 1". Let's try that.

fit = NonlinearModelFit[data, f[x], {a, b, {xa, 100}, {xb, 200}}, x];
fit // Normal // InputForm
(* Piecewise[{{1.1004729741760495*^-6, x < 200.73035367387615}, 
  {1.1004729741760495*^-6 - 2.914483888454594*^-9*(-200.73035367387615 + x), 
   200.73035367387615 <= x < 253.00000699926912}, 
  {9.481339117040847*^-7, 253.00000699926912 <= x}}, 0] *)

That's better.

Show[ListPlot[data], Plot[fit[x], {x, 0, 500}, PlotStyle -> {Red, Thick}]]

enter image description here

Community
  • 1