0

The following threads call our attention to the fact that "accuracy of Interpolation will be worse with an unstructured grid", in the context of interpolation of 3d data:

interpolation of 3D data

Improved interpolation of mostly-structured 3d data

I want to know if there is a systematic way to do the interpolation correctly for a 3D data with the points distributed logarithmically along x and y.

Simple example

The xy grid would be built using

grid = Table[ {10^t, 10^u}, {t, 1, 3, 0.05}, {u, 1, 3, 0.1}]
ListPlot[ grid ]

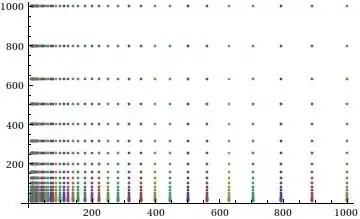
Logarithmic grid

Of course, in logarithmic scale it looks fine (linear):

ListLogLogPlot[ grid ]

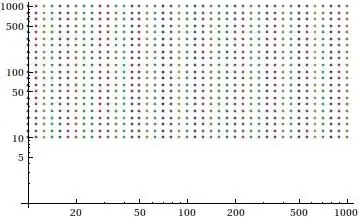
enter image description here

The 3D data would be built using some 2 variable function func:

tabx = Table[10^w, {w, 1, 3, 0.05}]
taby = Table[10^w, {w, 1, 3, 0.1}]
tab = Table[ {{x,y},func[x, y]}, {x, tabx}, {y, taby}]

Then, how to interpolate tab properly?

Community
  • 1
fcpenha
  • 738
  • 5
  • 16
  • Just using Interpolation works fine and gives high-order interpolation, although you have to use Flatten[tab, 1] to get rid of the nesting. It seems Mathematica still considers your data a structured grid, because it still has the structure of a full grid even though the $x$ and $y$ coordinates are nonuniformly sampled. –  Feb 15 '14 at 19:45
  • link This was very helpful to me. And I guess just find the log to get the uniform grid then organize the data as shown in the link. – Lina Feb 16 '14 at 01:10
  • I don't see any difference between using Interpolation and ListInterpolaton for multidimensional data. Is there any difference? Maybe I am missing something. – fcpenha Feb 16 '14 at 02:02
  • Nevertheless, your point about doing the interpolation on the uniform grid is good. – fcpenha Feb 16 '14 at 02:49
  • Sometimes I wonder why I bother to leave comments. –  Feb 16 '14 at 08:27
  • Dear Mr. Narain, if you believe your comment corresponds to the final answer, please add it as an answer. I assume you haven't got your 3k reputation with politeness. – fcpenha Feb 16 '14 at 14:12

0 Answers0