21

I have a 3D surface given in data-points of the form ${x,y,z}$. What is the easiest way to get the interpolated value $z=f(X,Y)$ for given coordinates ${X,Y}$ (which are of course not in the data list)?

Verbeia
  • 34,233
  • 9
  • 109
  • 224
pawel_winzig
  • 1,577
  • 1
  • 12
  • 21

2 Answers2

21

Mathematica's interpolation function, Interpolation, works on multidimensional data. For example,

data = Flatten[Table[{x, y, x^2 + y^2}, {x, -10, 10}, {y, -10, 10}], 1];
int = Interpolation[data];

Then, you can extract the values for values between the data points:

int[1.1, 1.1]
(* ==> 2.42 *)

And Plot3D, or whatever else you want.

Plot3D[int[x, y], {x, -10, 10}, {y, -10, 10}]

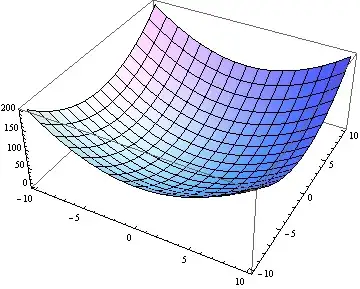
Mathematica graphics

Note, that the interpolation is pretty good:

exact[x_, y_] := x^2 + y^2
int[1.1, 1.1] == exact[1.1, 1.1]
(* => True *)

Or better yet (thanks @rcollyer):

(int[1.1, 1.1] - exact[1.1, 1.1])/exact[1.1, 1.1]
(* 1.83508*10^-16 *)

Update Leonid's comment below pointed out that the accuracy of Interpolation will be worse with an unstructured grid. For example:

dataDelete = Delete[data, RandomInteger[{1, Length[data]}]]
intD = Interpolation[dataDelete]

Then,

(intD[1.1, 1.1] - exact[1.1, 1.1])/exact[1.1, 1.1]
(* ==> 0.0743802 *)

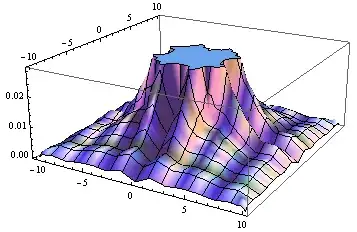
which is worse. It seems particularly bad close to the origin:

Plot3D[(intD[x, y] - exact[x, y])/ exact[x, y], {x, -10, 10}, {y, -10, 10}]

Mathematica graphics

Eli Lansey
  • 7,499
  • 3
  • 36
  • 73
  • What's the value of int[1.1, 1.1] - exact[1.1, 1.1]? That gives a better indication of fitness then Equal. – rcollyer Apr 26 '12 at 15:58
  • 5
    +1. Note that Interpolation only works on structured grids, while on unstructured ones the interpolation order will be reduced to 1, which in most cases will not be good enough. Try deleting one of the points from your regular grid to see what I mean. – Leonid Shifrin Apr 26 '12 at 16:03
  • @rcollyer Good call. I've updated my answer. – Eli Lansey Apr 26 '12 at 16:10
  • @LeonidShifrin right, and to get use an unstructured grid, one must rely on splines, likely NURBS. I have not used the mma functionality for that, though. – rcollyer Apr 26 '12 at 16:13
  • @LeonidShifrin Wow, it's much worse on an unstructured grid. I wonder if there's a (good) way to fill in the missing element to create a structured grid such that the interpolation is only really bad near the refilled grid point. – Eli Lansey Apr 26 '12 at 16:23
  • @EliLansey My guess is that this would depend on how unstructured a grid is. If it is mostly structured, but missing a few points, those points can probably be added using a linear interpolation to compute them, as a bootstrap. If, however, all grid is irregular, then some other method is obviously needed. – Leonid Shifrin Apr 26 '12 at 16:28
  • @LeonidShifrin Any idea how to figure out where the grid is missing points? Because then you could interpolate to first order, use that the fill the hole, then interpolate to higher order. – Eli Lansey Apr 26 '12 at 16:43
  • @EliLansey This sounds like a good candidate for a separate question :). – Leonid Shifrin Apr 26 '12 at 17:04
  • @LeonidShifrin Good idea – Eli Lansey Apr 26 '12 at 17:28
  • Please, if someone could help me with a closely related question... I may be experiencing a problem with interpolation of 3d data for x and y organized logarithmically. Is this the case of an "unstructured grid"? – fcpenha Feb 15 '14 at 04:52
17

Interpolation. Let's create some 100x3 data matrix, coloumns representing x, y and f(x,y), covering the domain from [1,10], sampled at the integers for both x and y

data = Join[Tuples[{Range[10], Range[10]}], RandomReal[20, {100, 1}], 
   2];

Now, I have to apply Interpolation to the data, but after grouping it as a list of {{x, y}, f[x,y]} values

f = Interpolation[Through@{Most, Last}[#] & /@ data];

You can use f as a regular function, if you keep inside the bounds of your sampling.

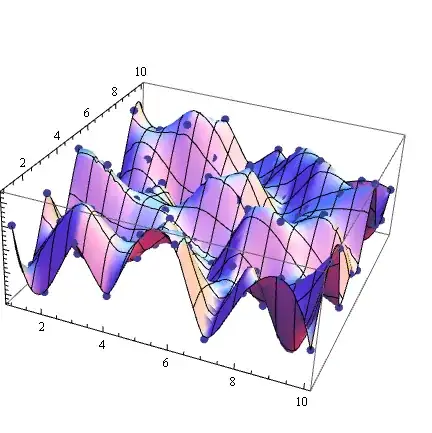
Let's see the results graphically 

Show[ListPointPlot3D[data, PlotStyle -> PointSize[Large]], 
 Plot3D[f[x, y], {x, 1, 10}, {y, 1, 10}]]

enter image description here

Rojo
  • 42,601
  • 7
  • 96
  • 188