How can I generate and randomly assign color to annular sectors?

Question

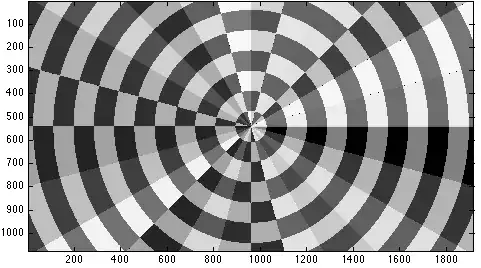
enter image description here

How can I generate such an image and fill every annular sector with a random colour?

ParametricPlot[r {Cos[t], Sin[t]}, {t, 0, 2 Pi}, {r, 0, 5}, MeshShading -> {{Red, Blue}, {Yellow, Green}}] ? — Szabolcs, Feb 25 '14 at 21:29
Related: http://mathematica.stackexchange.com/questions/10923/understanding-pie-chart-annulus-generation-and-alternate-style-using-disk — Sjoerd C. de Vries, May 25 '15 at 14:21

score 19 · Answer 1 · answered Feb 25 '14 at 21:32

Hmm...Szabolcs beat me to it (in a comment) by one minute...

plot = ParametricPlot[r {Cos[t], Sin[t]}, {r, 0, 12}, {t, 0, 2 Pi}, 
   Mesh -> 23, Axes -> False, 
   MeshShading -> {{Red, Green}, {Blue, Yellow}}, 
   PlotRange -> {{-9, 9}, {-4, 4}}];

plot /. poly_Polygon :> {RGBColor @@ RandomReal[1, 3], poly}

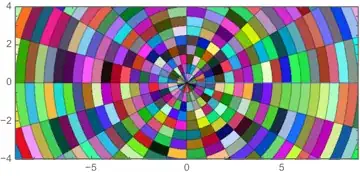
Mathematica graphics

score 18 · Accepted Answer · answered Oct 10 '14 at 18:07

18

With V10 came RandomColor and ColorSpace

Using Michael E2's wonderful solution

plot =
  ParametricPlot[r {Cos[t], Sin[t]}, {r, 0, 12}, {t, 0, 2 Pi},
   ImageSize -> 500,
   Mesh -> 13,
   MeshShading -> {{Red, Red}, {Red, Red}},
   PlotRange -> {{-9, 9}, {-4, 4}}];

Grid @ Partition[Table[plot /.
    poly_Polygon :> {RandomColor[ColorSpace -> space], poly},
         {space, {"RGB", "XYZ", "CMYK", "Grayscale"}}], 2]

enter image description here

answered Oct 10 '14 at 18:07

eldo

67,911
5
60
168

eldo, just saw this.. Neat (+1) – kglr Oct 10 '14 at 18:55
2

@eldo very nice...thank you for introducing me to RandomColor and ColorSpace :) – ubpdqn May 24 '15 at 08:15

score 15 · Answer 3 · answered Oct 10 '14 at 18:08

15

Making the MeshShading setting Dynamic also works without the need for post-processing:

ParametricPlot[r {Cos[t], Sin[t]}, {r, 0, 12}, {t, 0, 2 Pi},
 Mesh -> 23, Axes -> False,
 MeshShading -> Dynamic@{{Hue@RandomReal[], Hue@RandomReal[]},
                         {Hue@RandomReal[], Hue@RandomReal[]}}, 
 PlotRange -> {{-9, 9}, {-4, 4}}]

enter image description here

The same trick works in combination with V10 RandomColor:

ParametricPlot[r {Cos[t], Sin[t]}, {r, 0, 12}, {t, 0, 2 Pi},
  Mesh -> 23, Axes -> False,BaseStyle->Opacity[.75],
  MeshShading ->Dynamic@ {{RandomColor[], RandomColor[]}, 
                        {RandomColor[], RandomColor[]}}, 
  PlotRange -> {{-9, 9}, {-4, 4}}]

enter image description here

ParametricPlot[r {Cos[t], Sin[t]}, {r, 0, 12}, {t, 0, 2 Pi},
  Mesh ->{25,25}, Axes -> False, BaseStyle->Opacity[.75],
  MeshShading ->Dynamic@Evaluate@ Table[RandomColor[],{25},{2}], 
  PlotRange -> {{-9, 9}, {-4, 4}}]

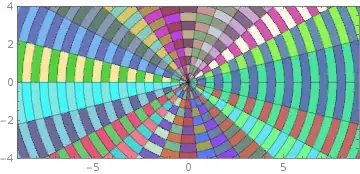
enter image description here

ParametricPlot[r {Cos[t], Sin[t]}, {r, 0, 12}, {t, 0, 2 Pi},
  Mesh ->{25,25}, Axes -> False, BaseStyle->Opacity[.75],
  MeshShading ->Dynamic@Evaluate@ Table[RandomColor[],{2},{25}], 
  PlotRange -> {{-9, 9}, {-4, 4}}]

enter image description here

answered Oct 10 '14 at 18:08

kglr

394,356
18
477
896

3

Surprising (your use of Dynamic), innovative and upvoteable :) – eldo Oct 10 '14 at 18:15
Could you please explain why this approach works? I'm surprised. +1, of course. – Alexey Popkov Oct 10 '14 at 18:59
@Alexey, i wish i knew why:) my vague hunch is that the FrontEnd -- as the owner/manager of Dynamic stuff -- triggers new calls to RandomReal/RandomColor since a given call changes something visible ..? Thanks for the vote by the way. – kglr Oct 10 '14 at 19:05
1

The InputForm of the output shows that every Polygon has the color specification Dynamic[Hue[RandomReal[]]. It means that the actual reason is inside the Kernel: it keeps the Dynamic head as the head for every color specification it produces from MeshShading. Very interesting and undocumented design decision! Does other plotting functions behave in the same way or only ParametricPlot? A documented way to get the same result is MeshShading->{{Dynamic@Hue@RandomReal[],Dynamic@Hue@RandomReal[]},{Dynamic@Hue@RandomReal[],Dynamic@Hue@RandomReal[]}}. – Alexey Popkov Oct 10 '14 at 19:27
@Alexey, interesting... I think it would work for other Chart/Plot functions. I have used it with ChartElementData stuff occassinally. – kglr Oct 10 '14 at 19:33
Note that MeshShading->{Dynamic@{Hue@RandomReal[],Hue@RandomReal[]},Dynamic@{Hue@RandomReal[],Hue@RandomReal[]}} does not work and produce an error message. It means that only when the Head of the entire MeshShading specification is Dynamic it is treated by the Kernel in a special way. – Alexey Popkov Oct 10 '14 at 19:38
1

We can also get the same result without Dynamic in the output: ParametricPlot[r {Cos[t],Sin[t]},{r,0,12},{t,0,2Pi},Mesh->23,Axes->False,MeshShading->Dynamic@{{Hue@RandomReal[],Hue@RandomReal[]},{Hue@RandomReal[],Hue@RandomReal[]}},PlotRange->{{-9,9},{-4,4}}]/.Dynamic->Identity. – Alexey Popkov Oct 10 '14 at 19:55

J. M.'s missing motivation · Answer 4 · 2020-05-21T00:58:36.133

For something somewhat different, I've elected to use BSplineCurve[] + FilledCurve[] to render each annular sector:

sector[{r1_?NumericQ, r2_?NumericQ}, {θ1_?NumericQ, θ2_?NumericQ}] /; r1 < r2 := 
 Module[{cc = Cos[(θ2 - θ1)/2], p1, p2, pm, sk = {0, 0, 0, 1, 1, 1}, sw},
        sw = {1, cc, 1};
        p1 = Through[{Cos, Sin}[θ1]]; 
        p2 = Through[{Cos, Sin}[θ2]];
        pm = Normalize[(p1 + p2)/2]/cc;
        Prepend[If[r1 == 0, {Line[{{0, 0}}]},
                   {Line[{r1 p2}],
                    BSplineCurve[r1 {pm, p1},
                                 SplineDegree -> 2, SplineKnots -> sk, SplineWeights -> sw],
                    Line[{r2 p1}]}],
                BSplineCurve[r2 {p1, pm, p2},
                             SplineDegree -> 2, SplineKnots -> sk, SplineWeights -> sw]]
        // FilledCurve]

(I discussed how to use NURBS to make circle arcs in this post.)

Generate the picture:

gr = BlockRandom[SeedRandom[42, Method -> "MersenneTwister"]; (* for reproducibility *)
            With[{n = 11, θh = π/12,
                  cn = 61 (* color scheme index *)},
                 Graphics[Table[{ColorData[cn,
                                 RandomInteger[{1, ColorData[cn, "Range"][[2]]}]], 
                                 sector[{r, r + 1}, {θ, θ + θh}]},
                                {r, 0, n}, {θ, 0, 2 π - θh, θh}], 
                          Frame -> True, PlotRange -> {{-9, 9}, {-4, 4}},
                          PlotRangeClipping -> True]]];

With smooth rendering:

Style[gr, FilledCurveBoxOptions -> {Method -> {"SplinePoints" -> 30}}]

smoothly rendered sectors

You can use version 10's RandomColor[] instead, if you want it.

Your annular sectors look very polygonal to me... But the colour scheme you picked is very pretty. — , May 24 '15 at 08:08
@Rahul, probably there is an internal setting that will make the B-splines look more circular, but I haven't found it yet... :( — J. M.'s missing motivation, May 24 '15 at 08:12

score 6 · Answer 5 · edited Apr 13 '17 at 12:55

An alternative method based on kguler's finding:

ParametricPlot[r {Cos[t], Sin[t]}, {r, 0, 12}, {t, 0, 2 Pi}, 
  Mesh -> 23, Axes -> False, MeshShading -> {{c, c}, {c, c}}, 
  PlotRange -> {{-9, 9}, {-4, 4}}] /. c :> Hue@RandomReal[]

plot

Note that as well as the kguler's answer this is based on undocumented details of the implementation of ParametricPlot and so will not necessarily work in future versions of Mathematica (but it works in v.8.0.4 and 10.0.1).

How can I generate and randomly assign color to annular sectors?

5 Answers5

Linked