2

I'm trying to explore how the zeros of a certain parameterized function change as its parameter changes.

dh[n_, k_, a_] := 
dh[n, k, a] = Sum[Binomial[k, j] dh[Floor[n/(m^(k - j))], j, m + 1], {m, a, n^(1/k)}, {j, 0, k - 1}]
dh[n_, 1, a_] := Floor[n] - a + 1
dh[n_, 0, a_] := 1
bn[ z_, a_] := bn[z, a] = Product[ (z - k), {k, 0, a - 1}]/a!
dd[n_, z_] := Sum[bn[z, a] dh[n, a, 2], {a, 0, Log[2, n]}]

The function I'm exploring here is dd[n_,z_].

n is the parameter I want to vary, and is a whole number $>= 1$. The zeros are all values of z such that dd[n,z] = 0. There should be $\log_2 n$ zeros for a given n.

Now, I already know that I can see the zeros for an isolated value of n as

zeros[n_] := List @@ NRoots[ dd[n, z] == 0, z][[All, 2]]

For example, if I try zeros[30], I get {-16.1801, -1.66598 - 0.772391 I, -1.66598 + 0.772391 I, -0.0879758}

I also know that I could visualize those zeros as

RootLocusPlot[1/dd[30, z], {k, 0, 1}]

But both of these techniques only address single values of n at a time. What I really want is to see how the zeros change as n changes, particularly for different scales of ranges for n.

Does Mathematica have any tools to help me do that?

J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574
Nathan McKenzie
  • 155
  • 5

1 Answers1

2

Building on Peltio's idea:

colfunc = ColorData["AvocadoColors"];
pts = Table[{colfunc[n/30], Point[{Re[#], Im[#]}]} & /@ zeros[n], {n, 5, 30}];
Graphics[pts, Frame -> True]

The color function is meant to give you an idea of which n a root correspond to. Of course it is optional, without it it's just Peltio's code.

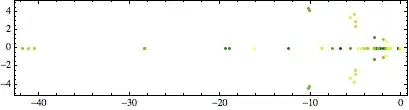
roots

The most beautiful visualization of roots I've seen on here is this.

Community
  • 1
C. E.
  • 70,533
  • 6
  • 140
  • 264