Nested list to graph

Question

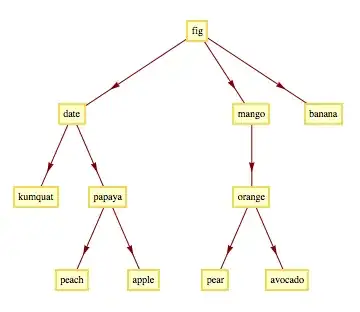
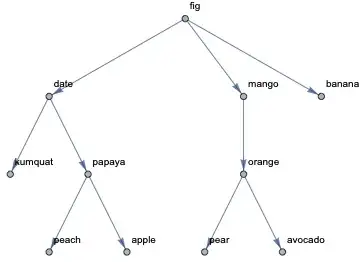
The following nested list can be regarded as a representation of a (tree) graph:

li = {"fig", {"date", {"kumquat"}, {"papaya", {"peach"}, {"apple"}}},
             {"mango", {"orange", {"pear"}, {"avocado"}}}, 
             {"banana"}}

In the above, a string is a node in the tree, and any lists that follow it are subtrees rooted at that node.

What are some of the ways by which this can be converted into a graph (or more concretely, a list of DirectedEdges)? I've come up with one way, listed below. But I wanted to learn about other interesting approaches - for instance, pattern replacements might be used?

This is what I came up with:

h[{str_String}] := Sequence[];
h[{str_String, ls__List}] := {DirectedEdge[str, #[[1]]], h@#} & /@ {ls};

edges = Flatten@h@li

(* 
{"fig" \[DirectedEdge] "date", "date" \[DirectedEdge] "kumquat", 
 "date" \[DirectedEdge] "papaya", "papaya" \[DirectedEdge] "peach", 
 "papaya" \[DirectedEdge] "apple", "fig" \[DirectedEdge] "mango", 
 "mango" \[DirectedEdge] "orange", "orange" \[DirectedEdge] "pear", 
 "orange" \[DirectedEdge] "avocado", "fig" \[DirectedEdge] "banana"}
*)

TreePlot[Rule @@@ edges, Automatic, "fig", DirectedEdges -> True, 
 VertexLabeling -> True]

Don't you wish this were an actual tree?

score 10 · Accepted Answer · edited Mar 13 '14 at 10:34

10

edges = Cases[li,
   {node_String, subtrees__List} :> (
     node \[DirectedEdge] #[[1]] & /@ {subtrees}),
   {0, ∞}] // Flatten

Note the level specification within Cases.

Graph[edges,
 VertexLabels -> "Name",
 ImagePadding -> 30,
 GraphLayout -> {
   "LayeredEmbedding",
    "RootVertex" -> "fig"}]

edited Mar 13 '14 at 10:34

ciao

25,774
2
58
139

answered Mar 13 '14 at 10:28

BoLe

5,819
15
33

score 4 · Answer 2 · answered Dec 10 '18 at 17:41

4

With IGraph/M running on Mathematica 11.3,

IGExpressionTree[li /. List -> Construct]

answered Dec 10 '18 at 17:41

Szabolcs

234,956
30
623
1,263

score 3 · Answer 3 · answered Jun 23 '14 at 17:34

3

li //. {{x_, rest__} :> x[rest], {x_} :> x} // 
 TreeForm[#, DirectedEdges -> True] &

enter image description here

A similar rule can be used to parse JSON data and display with TreeForm

answered Jun 23 '14 at 17:34

alancalvitti

15,143
3
27
92

1

If the goal was just produce a visual tree, then this would do fine... but the question was about converting the nested list representation to a "true" graph. – Aky Jun 23 '14 at 19:13

score 2 · Answer 4 · answered Mar 15 '14 at 11:35

2

Here's another way I think is interesting:

Flatten@Rest@
  Reap@Scan[Sow[Thread[First@# \[DirectedEdge] First /@ Rest@#]] &, 
    li, {0, -3}]

answered Mar 15 '14 at 11:35

Aky

2,719
12
19

score 1 · Answer 5 · answered May 17 '20 at 19:03

This doesn't directly answer the question, but can be used to create a tree graph from nested lists without the header element at each level. For example, lists such as {{a, {b, c}}, {d, e}}. Moreover, it represents internally each level of the graph with the hash of the corresponding expression, thus the generated graph identifies nodes corresponding to the same expression.

nestedListToGraph[expr_] := Reap[
  Map[
    CompoundExpression[
      Sow[Hash@#, "vertices"],
      If[Head@# =!= List, 
        Sow[Rule[Hash@#, ToString@#], "labels"]
      ],
      If[Head@# == List,
        Function[elem,
          Sow[DirectedEdge[Hash@#, Hash@elem], "edges"]
        ] /@ #
      ],
      #
    ] &,
    {expr}, Infinity
  ],
  {"vertices", "edges", "labels"}
] // Last // Map@First // Graph[#[[1]], #[[2]], VertexLabels -> #[[3]]] &;

SetProperty[
  nestedListToGraph@{{a, {b, c}}, {d, e}},
  GraphLayout -> "LayeredDigraphEmbedding"
]

Nested list to graph

5 Answers5

Linked