I would like to have a function circle which takes two inputs: a tuple {x,y} and a real number r and outputs the cooridinates of points on the circumference of a circle that is centered at $(x,y)$ which has radius $r$.
Importantly, I want the points to be equidistant on the circle.
I tried to implement the procedure here described as Circle Point Picking. But I don't get equidistant points.
Kindly help me. Here is the code I tried:
num = 20; r = 50;
circle = Module[{},
random = RandomReal[{-2, 2}, {num + 10, 2}];
random = Take[DeleteCases[random, #1^2 + #2^2 >= r^2 &], num];
Table[r {(x[[1]]^2 - x[[2]]^2)/(x[[1]]^2 + x[[2]]^2),
2 x[[1]] x[[2]]/(x[[1]]^2 + x[[2]]^2)}, {x, random}]
]
The above code will output num=20 points on a circle that are not equidistant on the circumference. Here is the output represented as a ListPlot:
ListPlot[circle]
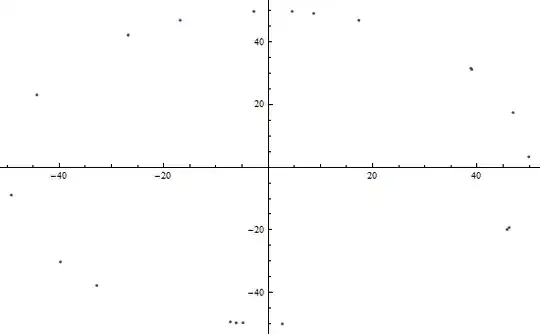
Irrelevant as such for the question, but if anyone is curious:
The context for getting equidistant points is that I want to embed a graph with some vertices located on the points. If you instead know how to do this, kindly tell me. I cannot find a use for CircularEmbedding because I only want a circular embedding on some vertices of the graph, not all vertices. The only way I see is to explicitly give the vertex cooridinates as points on a circle.





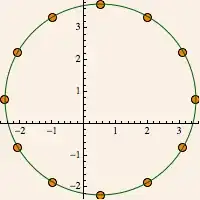
circle = Table[{r Cos[2 \[Pi]/num *(i - 1)], r Sin[2 \[Pi]/num *(i - 1)]}, {i, 1, num + 1}]. – Pavithran Iyer Mar 21 '14 at 03:50Pointin the function above. – ubpdqn Mar 21 '14 at 03:53