Monte Carlo integration with random numbers generated from a Gaussian distribution

Question

I want to do numerical integration of some functions using the Monte Carlo method. The default setting for the Monte Carlo method is to use a uniform distribution as far as I know.

How can I change the random number generation to Gaussian when doing numerical integration?

Answer 1

Because of the comment by @ciao I think it is a good idea to give a solution/answer using MonteCarloRule and PointGenerator.

PointGenerator is an object that expects a sub-value function definition for "MakePoint" with the signature:

"MakePoint"[dim_, totalNumberOfPoints_, i_, wprec_]

where the arguments are:

1. dim - integration dimension,
2. totalNumberOfPoints - desired total number of points per rule application,
3. i - point index,
4. wprec - working precision.

Note that "MakePoint" provides very fine granularity, it makes only one point. For optimization purposes custom definitions (like the one given below) have to provide some sort of optimization for generating a bulk of points. The consequence of such an approach is that if AdaptiveMonteCarlo is used then the sampling points of each application of MonteCarloRule are going to be rescaled versions of the same set of points.

Here are definitions that make PointGenerator work with a general distribution argument.

ClearAll[MCAbscGenerator, MCDistributionPoints];
MCDistributionPoints[distr_, dim_, totalNumberOfPoints_] :=
  MCDistributionPoints[distr, dim, totalNumberOfPoints] =
   Block[{points = RandomVariate[distr, {totalNumberOfPoints, dim}]},
    Transpose[
     Map[Rescale[#, {Min[#], Max[#]}, {0, 1}] &, 
      Transpose[points]]]];
MCAbscGenerator["MakePoint"[dim_, totalNumberOfPoints_, n_, wprec_]] :=
    MCDistributionPoints[NormalDistribution[], dim, 
    totalNumberOfPoints][[n]];
MCAbscGenerator[distr_][
  "MakePoint"[dim_, totalNumberOfPoints_, i_, wprec_]] :=
 MCDistributionPoints[distr, dim, totalNumberOfPoints][[i]];

(The definitions are probably not very didactic, but I think they provide good general properties: signatures and funcitonality.)

Here is how we apply the custom point generator with MonteCarloRule:

NIntegrate[x^2 + y^3, {x, 0, 1}, {y, 0, 1}, PrecisionGoal -> 2,
   Method -> {"MonteCarlo", 
   Method -> {"MonteCarloRule", 
     "PointGenerator" -> 
      MCAbscGenerator[TruncatedDistribution[{-1, 1}, NormalDistribution[]]]}}]

(* 0.561876 *)

The real value is 7/12:

Integrate[x^2 + y^3, {x, 0, 1}, {y, 0, 1}] // N

(* 0.583333 *)

Let us visualize the sampling points for different truncated versions of the Normal Distribution and different Monte-Carlo methods. Notice that the integral gets more underestimated for the wider truncated distribution ranges.

Needs["Integration`NIntegrateUtilities`"]

ds = {TruncatedDistribution[{-1, 1}, NormalDistribution[]], 
   TruncatedDistribution[{-2, 2}, NormalDistribution[]], 
   TruncatedDistribution[{-3, 3}, NormalDistribution[]], NormalDistribution[]};
Grid[Riffle[Table[{Style[distr, Blue], SpanFromLeft}, {distr, ds}], 
  Table[(est =
     NIntegrate[x^2 + y^3, {x, 0, 1}, {y, 0, 1}, PrecisionGoal -> 2, 
      Method -> {meth, 
        Method -> {"MonteCarloRule", 
          "PointGenerator" -> MCAbscGenerator[distr]}}];
    gr = NIntegrateSamplingPoints@
      NIntegrate[x^2 + y^3, {x, 0, 1}, {y, 0, 1}, PrecisionGoal -> 2, 
       Method -> {meth, 
         Method -> {"MonteCarloRule", 
           "PointGenerator" -> MCAbscGenerator[distr]}}];
    Labeled[Append[gr, Frame -> True], 
     Grid[{{"method:", meth}, {"estimate:", est}}]]
    ), {distr, ds}, {meth, {"MonteCarlo", "AdaptiveMonteCarlo"}}]], 
 Dividers -> {None, {{True, False}}}]

Answer 2

So I took the code that is on the Wikipedia page and corrected one problem (why it had 1.1*x - 0.1 instead of x is beyond me, but it throws the answer way off), and then rewrote it to be more general and (to me) easier to read.

Here is the function,

monteCarloGaussian[func_, x1_, x2_, n_, mean_: 0, σ_: 1] := 
 1/2 (Erf[(mean - x2)/(Sqrt[2] σ), (mean - x1)/(
    Sqrt[2] σ)]) 
    Mean[(func[#]/(E^(-((-mean + #)^2/(2 σ^2)))/(
       Sqrt[2 π] σ)) ) & /@ 
    RandomVariate[
     TruncatedDistribution[{x1, x2}, 
      NormalDistribution[mean, σ]], n]]

The arguments are a pure function to be integrated, the limits of integration, the number of points to sample, and optionally the mean and standard deviation of the underlying normal distribution. The prefactor is the integral of the normal distribution over the given range, and the integral is the sum of the function evaluated at the random points divided by their probability density at that point.

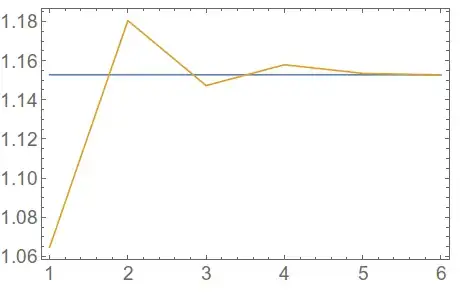
You can evaluate it for some functions and see how large a sample is needed for convergence,

exact = NIntegrate[1/(1 + Sinh[2 x] Log[x]^2), {x, 0, 2}]; 
Table[{exact, 
    monteCarloGaussian[Function[x, 1/(1 + Sinh[2 x] Log[x]^2)], 0, 
     2.0, n]}, {n, 10^Range[1, 6]}] // Transpose // ListLinePlot

When the limits of integration are far from zero, it is necessary to change the mean and standard deviation of the distribution:

exact = NIntegrate[1/(1 + Sinh[2 x/4] Log[x/2]^2), {x, 5, 10}]; 
Table[{exact, 
    monteCarloGaussian[Function[x, 1/(1 + Sinh[2 x/4] Log[x/2]^2)], 5,
      10.0, n]}, {n, 10^Range[1, 6]}] // Transpose // ListLinePlot

that looks bad, but this

exact = NIntegrate[1/(1 + Sinh[2 x/4] Log[x/2]^2), {x, 5, 10}]; 
Table[{exact, 
    monteCarloGaussian[Function[x, 1/(1 + Sinh[2 x/4] Log[x/2]^2)], 5,
      10.0, n, 7.5, 5]}, {n, 10^Range[1, 6]}] // 
  Transpose // ListLinePlot

is much better.

It should be straightforward to extend this for functions of multiple variables, and I can do that if there is interest.

The above function is optimized to use a normal distribution, but we could modify it to use any distribution,

monteCarloDist[func_, x1_, x2_, n_, dist_: NormalDistribution[0, 1]] :=
 Module[{int, vars, probs},
  int = Integrate[PDF[dist, xx], {xx, x1, x2}];
  vars = RandomVariate[
    TruncatedDistribution[{x1, x2},
     dist], n];
  probs = PDF[dist, vars];
   int  Mean[(func[#1]/#2 ) & @@@ Transpose[{vars, probs}]]
  ]

With this you can use any of the built-in or user-defined distribution functions. It is a little slower than the one above for a NormalDistribution since it has to work out the integral on its own and it has to get the probabilities on its own, but not too much slower. The more complicated you make your distribution, the longer it takes,

exact = NIntegrate[1/(1 + Sinh[2 x] Log[x]^2), {x, 0, 2}];
Table[{exact, 
    monteCarloDist[Function[x, 1/(1 + Sinh[2 x] Log[x]^2)], 0, 2.0, n,
      ProbabilityDistribution[Sqrt[2]/Pi/(1 + x^4), {x, -4, 4}]]}, {n,
     10^Range[1, 6]}] // Transpose // ListLinePlot