Can I enter the traditional form for Binomial as input in an expression?

Question

Is there a way to enter the traditional form of a binomial coefficient, i.e. ${n \choose k}$ instead of Binomial[n,k], like I would enter a radical sign $\sqrt{x}$ using Ctrl-Shift-2? I would like to enter it that way in a notebook, and see it in that form in the input as well as output equations, just like the radical. I know that I can use TraditionalForm to convert it on output, but I don't need to do that to see radicals instead of Sqrt.

Answer 1

You could do it using the following (this is the first version of the answer; don't use it if you want the more complete solution below):

SetOptions[EvaluationNotebook[],InputAliases->{"bn"->
 FormBox[TemplateBox[{"\[SelectionPlaceholder]",
  "\[Placeholder]"},"Binomial"],InputForm]}]

Then enter escbnesc to get a placeholder that you can tab through:

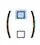
Then enter the numbers and press shift-enter to evaluate.

Edit

To make the output appear formatted without invoking TraditionalForm, you'd have to define a wrapper function and its style. I'll set the keyboard shortcut in a way that doesn't erase previous definitions.

ClearAll[myBinomial]

appearance[x_, y_] := TemplateBox[{x, y}, "myBinomial",
  DisplayFunction :> (RowBox[{"(", "\[NoBreak]", 
       GridBox[{{#1}, {#2}}, RowSpacings -> 1, ColumnSpacings -> 1, 
        RowAlignments -> Baseline, ColumnAlignments -> Center], 
       "\[NoBreak]", ")"}] &), 
  InterpretationFunction :> (RowBox[{"myBinomial", "[", 
       RowBox[{#1, ",", #2}], "]"}] &)
  ]

myBinomial[n_?NumericQ, k_?NumericQ] := Binomial[n, k]

myBinomial /: MakeBoxes[myBinomial[n_, k_], StandardForm] := 
 appearance[ToBoxes[n], ToBoxes[k]]

SetOptions[EvaluationNotebook[], 
 InputAliases -> 
  DeleteDuplicates@
   Join[{"bn" -> 
      appearance["\[SelectionPlaceholder]", "\[Placeholder]"]}, 
    InputAliases /. 
      Quiet[Options[EvaluationNotebook[], InputAliases]] /. 
     InputAliases -> {}]
 ]

Now the template appears as before, but when the function arguments aren't numerical, it's also displayed in 2D form. One could add additional definitions to myBinomial depending on what cases you want the 2D display to apply to. Whenever there is no definition for myBinomial, it is left unevaluated and will be displayed in the formatted style.

Update in response to comment:

Similar templates can also be created for other two-dimensional symbols using other types of brackets. As an example, here are shortcuts for StirlingS1 and StirlingS2 that can be entered as escs1esc and escs2esc:

appearanceS1[x_, y_] := 
 TemplateBox[{x, y}, "myStirlingS1", 
  DisplayFunction :> (StyleBox[
      RowBox[{"[", "\[NoBreak]", 
        GridBox[{{#1}, {#2}}, RowSpacings -> 1, ColumnSpacings -> 1, 
         RowAlignments -> Baseline, ColumnAlignments -> Center], 
        "\[NoBreak]", "]"}], SpanMaxSize -> Infinity] &), 
  InterpretationFunction :> (RowBox[{"myStirlingS1", "[", 
       RowBox[{#1, ",", #2}], "]"}] &)]

myStirlingS1[n_?NumericQ, k_?NumericQ] := StirlingS1[n, k]

myStirlingS1 /: MakeBoxes[myStirlingS1[n_, k_], StandardForm] := 
 appearanceS1[ToBoxes[n], ToBoxes[k]]

appearanceS2[x_, y_] := 
 TemplateBox[{x, y}, "myStirlingS2", 
  DisplayFunction :> (StyleBox[
      RowBox[{"{", "\[NoBreak]", 
        GridBox[{{#1}, {#2}}, RowSpacings -> 1, ColumnSpacings -> 1, 
         RowAlignments -> Baseline, ColumnAlignments -> Center], 
        "\[NoBreak]", "}"}], SpanMaxSize -> Infinity] &), 
  InterpretationFunction :> (RowBox[{"myStirlingS2", "[", 
       RowBox[{#1, ",", #2}], "]"}] &)]

myStirlingS2[n_?NumericQ, k_?NumericQ] := StirlingS2[n, k]

myStirlingS2 /: MakeBoxes[myStirlingS2[n_, k_], StandardForm] := 
 appearanceS2[ToBoxes[n], ToBoxes[k]]

SetOptions[EvaluationNotebook[], 
 InputAliases -> 
  DeleteDuplicates@
   Join[{"s1" -> 
      appearanceS1["\[SelectionPlaceholder]", "\[Placeholder]"], 
     "s2" -> appearanceS2["\[SelectionPlaceholder]", 
       "\[Placeholder]"]}, 
    InputAliases /. 
      Quiet[Options[EvaluationNotebook[], InputAliases]] /. 
     InputAliases -> {}]
 ]

In these definitions, I added one additional ingredient: the square and curly brackets for these symbols are not automatically extensible, so they don't grow like the round brackets used in Binomial. To fix this, I added a StyleBox with option SpanMaxSize -> Infinity.

Also, the shortcuts are be appended to the InputAliases without erasing previous definitions. To make the shortcuts work, this step has to be done after defining the wrapper functions appearance and appearanceS1/S2.

With this, you can get output like this:

for StirlingS1 and

for StirlingS2.