region plot in a 2-simplex

Question

I want to plot a 2-dimensional region with constraint $x+y\le N$, i.e., I want to plot a sub-region inside a 2-simplex.

As an example:

Module[{n = 300, p = 0.5},
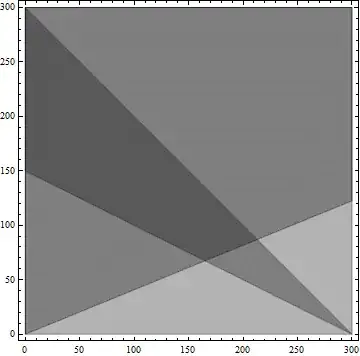
RegionPlot[{y > (1/2)*(n - x) && y + x <= n && y > p/(1 - p)*x}, 
{x, 0, n}, {y, 0, n}, FrameLabel -> {"x", "y"}, 
PlotStyle -> {Yellow, Opacity[0.5]}]]

What should I do to transform the region to a 2-simplex?

Edit 1 & 2 & 3

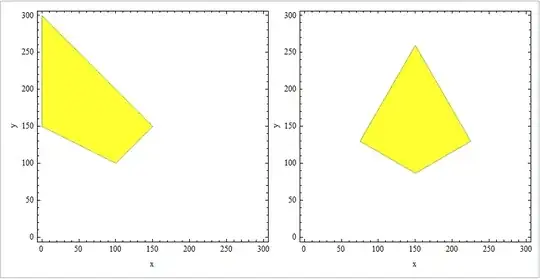
The command above will give you the following plot:

enter image description here

which clearly satisfies the $x+y\le N$ constraint. So I want a coordinate transform that changes the shape of the yellow area into the shape of the red area in the plot below (it is from Matlab):

enter image description here

It's hard to tell what you're asking. Your plot already lies in the 2-simplex $x\ge0,y\ge0,x+y\le N$. Are you looking for a plot that looks like an equilateral triangle? Please explain what you mean by "transform the region into a 2-simplex". — , Apr 17 '14 at 16:39
@RahulNarain, it's certainly related, but the OP seemed to want something rather advanced. I have a very difficult time extracting what I need from the post. — wdg, Apr 17 '14 at 17:16
guys, I have reworded the question and hope this time it is clear. — wdg, Apr 18 '14 at 01:24
@SjoerdC.deVries, sorry the value of $p$ should be 0.5. My intent is to see how the shape of the area changes with $p$. Yes, I want a coordinate transform. I have modified the question accordingly. — wdg, Apr 18 '14 at 13:37

score 7 · Accepted Answer · edited Apr 13 '17 at 12:55

rp = Module[{n = 300, p = 0.5}, 
  RegionPlot[{y > (1/2)*(n - x) && y + x <= n && y > p/(1 - p)*x},
     {x, 0, n}, {y, 0, n}, FrameLabel -> {"x", "y"}, PlotPoints -> 100,
     PlotStyle -> Directive[Yellow, Opacity[0.8]], ImageSize -> 300]];
toSimplex = #1 {1, 0} + #2 {1, Sqrt[3]}/2 &;
Panel@Row[{rp, MapAt[toSimplex @@ # &, rp, {{1, 1, ;;}}]}]

enter image description here

rp2 = Module[{n = 300, p = 0.5},  RegionPlot[{y > (1/2)*(n - x) && y + x <= n && 
    y > p/(1 - p)*x,  x + y < n}, {x, 0, n}, {y, 0, n}, FrameLabel -> {"x", "y"}, 
    PlotStyle -> {Directive[Yellow, Opacity[0.8]], Directive[White, Opacity[0.1]]},
    PlotPoints -> 100, ImageSize -> 300]];
Panel@Row[{rp2, MapAt[toSimplex @@ # &, rp2, {{1, 1, ;;}}]}]

Note: In version 9, one can use Span objects in the third argument of MapAt as first noted in this answer by Kuba.

enter image description here

You can also use

tF = FindGeometricTransform[{{0, 0}, {1, 0}, {1, Sqrt[3]}/2},
     {{0, 0}, {1, 0}, {0, 1}}][[2]];
MapAt[GeometricTransformation[#, tF] &, rp2, {1}] //Panel

enter image description here

Would you care to elaborate on the rather uncommon syntax of your MapAt call? — Sjoerd C. de Vries, Apr 18 '14 at 16:38
@Sjoerd, thanks. Updated and added a reference to Kuba's answer regarding the MapAt usage with Spans. ({{}} in the original was a copy/paste error.) — kglr, Apr 18 '14 at 16:54

score 0 · Answer 2 · edited Sep 14 '15 at 08:32

0

Maybe this will be helpful:

Module[{n=300,p=0.29,r1,r2,r3,r4,x,y},
r1=y>(1/2)*(n-x);
r2=y+x<=n;
r3=y>p/(1-p)*x;
(*RegionPlot[#,{x,0,n},{y,0,n},PlotStyle\[Rule]Opacity[.3]]&/@{r1,r2,r3}*)
Show[RegionPlot[#,{x,0,n},{y,0,n},PlotStyle->Opacity[.3]]&/@{r1,r2,r3}]
]

code result

edited Sep 14 '15 at 08:32

tinlyx

115
1
6

answered Apr 17 '14 at 13:30

molekyla777

2,888
1
14
28

region plot in a 2-simplex

2 Answers2

Linked