I tried to plot plane $x = 0$ and $y=0$ with Plot3D[x = 0, {x, -4, 4}, {y, -4, 4}] but it seems that it didn't work out. How can I plot the above planes?
Also is there a way to plot with z parameter being in the function? Note: I was trying to illustrate a closed surface by planes x=0,y=0,z=0 and 2x+2y+z=4
Definitons from Planetmath
We may show that a first-degree equation \begin{align} Ax+By+Cz+D = 0 \end{align} between the variables $x$, $y$, $z$ represents always a plane. In fact, we may without hurting generality suppose that, $D \leqq 0$. Now $R := \sqrt{A^2+B^2+C^2} > 0$. Thus the length of the radius vector of the point, $(A,B,C)$, is $R$. Let the angles formed by the radius vector with the positive coordinate axes be $\alpha$, $\beta$, $\gamma$. Then we can write $$A = R\cos\alpha, \quad B = R\cos\beta, \quad C = R\cos\gamma$$ (cf. direction cosines). Dividing first degree equation term wise by $R$ gives us $$x\cos\alpha+y\cos\beta+z\cos\gamma+\frac{D}{R} = 0,$$ where, $\frac{D}{R} \leqq 0$. The last equation represents a plane whose distance from the origin is $-\frac{D}{R}$ and whose normal line forms the angles $\alpha$, $\beta$, $\gamma$ with the coordinate axes.
Since the coefficients $A,B,C$ are proportional to the direction cosines of the normal vector of this plane, they are direction numbers of the normal line of the plane.
Examples
The equations of the coordinate planes are $x = 0$ ($yz$-plane); $y = 0$ ($zx$-plane), $z = 0$ ($xy$-plane); the equation of the plane through the points, $(1,0,0)$, $(0,1,0)$, and $(0,0,1)$ is $x+y+z = 1$.
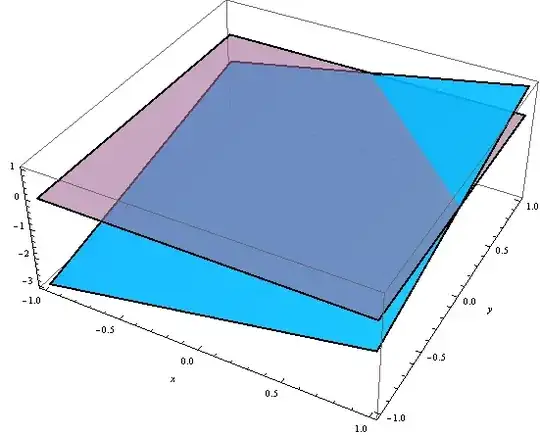
Try this for $z=0$ and $x+y+z=1$.
f[x_, y_] = 0;
Plot3D[{f[x, y], x + y - 1}, {x, -1, 1}, {y, -1, 1}, Mesh -> None,AxesLabel ->
Automatic,PlotStyle -> {{Directive[Pink, Opacity[0.6],
Specularity[White, 40]]}, {Directive[Cyan, Opacity[0.9],
Specularity[White, 10]]}},BoundaryStyle -> Directive[Black, Thick]]
Your Problem
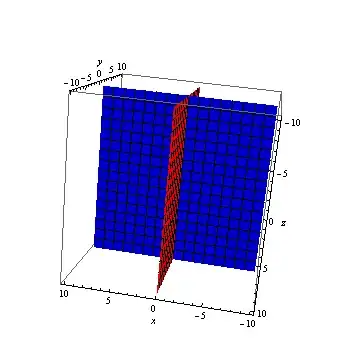
Now lets plot the plane $2 x + 2 y + z =4$ that you want with the planes $x=0,y=0$
ContourPlot3D[Evaluate@{2 x + 2 y + z == 4, {0, y, 0}, {x, 0, 0}},
{x, -1, 1}, {y, -1, 1}, {z, -1, 1},
BoundaryStyle -> Directive[Black, Thick],
MeshStyle -> Directive[Red, Thickness@0.003],
MeshFunctions -> (Total[{0, 0, #3}] &),
ColorFunction ->
Function[{x, y, z, f}, Evaluate[Hue[#] & /@ {x, y, z}]],
AxesLabel -> Automatic, Boxed -> False,
ContourStyle -> Directive[Opacity[0.6], Specularity[White, 30]],
ColorFunctionScaling -> False]
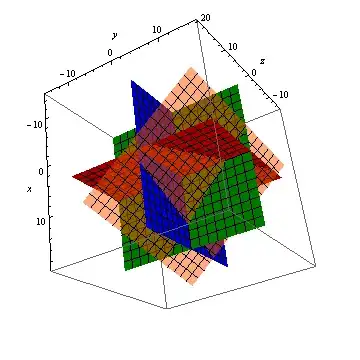
You can also use RegionPlot the see the 3D area enclosed by these three planes namely $xy,yz,zx$ that are meshed with white lines.
pic = RegionPlot3D[2 x + 2 y + z < 4, {x, -0, 1}, {y, 0, 1}, {z, 0, 8},
BoundaryStyle -> Directive[Black, Thick], Mesh -> None,
PlotStyle -> Directive[Yellow, Opacity[0.9]],
ColorFunction -> "BlueGreenYellow", AxesLabel -> Automatic,
Boxed -> False];
Show[pic, ContourPlot3D[
Evaluate@{{x, 0, 0}, {0, y, 0}, {0, 0, z}}, {x, -0, 1}, {y, 0, 1}, {z, 0, 8},
BoundaryStyle -> Directive[White, Thick],
MeshStyle -> Directive[White, Thickness@0.003],
ColorFunction -> Function[z, RGBColor[z, 1 - z, 1]],
AxesLabel -> Automatic, Boxed -> False]]
You can plot the two planes using ParametricPlot3D.
Here is an example
ParametricPlot3D[{{0, u, v}, {u, 0, v}}, {u, -10, 10}, {v, -10, 10},
PlotStyle -> {Red, Blue}, AxesLabel -> {x, y, z}, ImagePadding -> 60]
The xy plane is coloured red and the yz blue.
Here is the space you wanted to visualize:
i = {1, 0, 0}; j = {0, 1, 0}; k = {0, 0, 1};
n = {2, 2, 1}; d = 4;
r = RotationMatrix[{i, n}];
jc = r.j; kc = r.k;
ParametricPlot3D[{{0, u, v}, {u, 0, v}, {u, v, 0},
jc*u + kc*v + d}, {u, -15, 15}, {v, -15, 15},
PlotStyle -> {Red, Blue, Green, Directive[Orange, Opacity[.5]]},
AxesLabel -> {x, y, z}, ImagePadding -> 60]
This works by first finding two orthogonal unit vectors on the plane (jc and kc). The vectors are found by using a rotation matrix that rotates the i unit vector along the direction of the plane normal vector n. If the same rotation matrix is applied to j and k we get the correct unit vectors on the plane.
Taking into account the edit of the post you need RegionPlot3D, e.g.
RegionPlot3D[ 2 x + 2 y + z - 4 <= 0, {x, 0, 2}, {y, 0, 2}, {z, 0, 4},
PlotStyle -> Directive[Lighter @ Green, Opacity[0.2]], AxesLabel -> Automatic]
or making it more transparent we reduce slightly mesh lines :
RegionPlot3D[ 2 x + 2 y + z - 4 <= 0, {x, 0, 2}, {y, 0, 2}, {z, 0, 4},
PlotStyle -> Directive[ Cyan, Opacity[0.1], Specularity[0.9]],
AxesLabel -> Automatic, Mesh -> {0, 0, 3} ]
or making use of ContourPlot3D, e.g.
ContourPlot3D[ 2 x + 2 y + z == 4, {x, 0, 2}, {y, 0, 2}, {z, 0, 4}, MeshFunctions -> {#3 &}]
and plotting x == 0, y == 0, ...
ContourPlot3D[{ x == 0, y == 0, z == 0}, {x, 0, 4}, {y, 0, 4}, {z, 0, 4},
MeshFunctions -> {#3 &}, ContourStyle -> Opacity[0.35],
RegionFunction -> Function[{x, y, z}, 2 x + 2 y + z - 4 <= 0]]
Also is there a way to plot with z parameter being in the function?
If you are asking for a method to plot an arbitrary surface, you can use ParametricPlot3D which allows you to specify an arbitrary expression for the {x,y,z} coordinates, and have this span two parameters to form a surface.
ParametricPlot3D[v1 {10,0}+v2{0,1,1}, {v1, -1, 1}, {v2, -1, 1}]
RegionPlot, see my answer. – Artes Jun 19 '12 at 10:01