Update 2
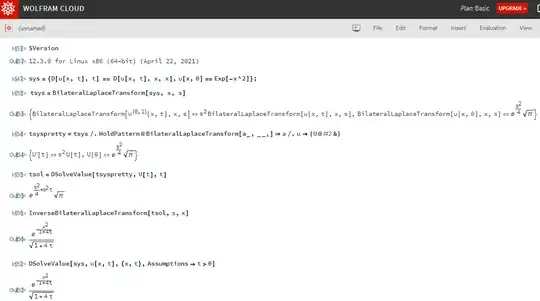
In v12.3, BilateralLaplaceTransform and InverseBilateralLaplaceTransform are built-in. Their usages are almost the same as the ones defined in this post. Example:
sys={D[u[x, t], t] == D[u[x, t], x, x],u[x,0]==Exp[-x^2]};
tsys=BilateralLaplaceTransform[sys, x, s]
tsyspretty=tsys/.HoldPattern@BilateralLaplaceTransform[a_,__]:>a/.u->(U@#2&)
tsol=DSolveValue[tsyspretty,U[t],t]
InverseBilateralLaplaceTransform[tsol,s,x]
(* For comparison: *)
DSolveValue[sys,u[x,t],{x,t},Assumptions->t>0]
Update
First I'd like to mention that after checking the definition of bilateral Laplace transform and Fourier transform carefully, I'm sure currently the formula for the relationship between them on the wikipedia page is wrong, the correct one should be:
$$\mathcal{B}\{f(t)\}(s) = \sqrt{2\pi}\mathcal{F}\{f(t)\}(is)$$
Then we can use the internal function FourierTransform to implement the bilateral Laplace transform. Mathematica's FourierTransform, unlike LaplaceTransform, isn't that handy, so we need to use the "shell" in this post to enhance it:
mft[(h : List | Plus | Equal)[a__], t_, w_] := (mft[#1, t, w] &) /@ h[a]
mft[a_ b_, t_, w_] /; FreeQ[b, t] := b mft[a, t, w]
mft[a_, t_, w_] := Sqrt[2 π] FourierTransform[a, t, w]
mift[(h : List | Plus | Equal)[a__], t_, w_] := (mift[#1, t, w] &) /@ h[a]
mift[a_ b_, t_, w_] /; FreeQ[b, t] := b mift[a, t, w]
mift[a_, t_, w_] := InverseFourierTransform[a, t, w]/Sqrt[2 π]
BilateralLaplaceTransform[expr_, t_, s_] := mft[expr, t, s I]
InverseBilateralLaplaceTransform[expr_, s_, t_] :=
Module[{ω}, mift[expr /. s -> ω/I, ω, t]]
Remark
mft is short for modified Fourier transform and mift is short for modified inverse Fourier transform.
- I choose to manually add the $\sqrt{2 \pi }$ term rather than setting a
FourierParameter because currently InverseFourierTransform can't handle it properly, for example
InverseFourierTransform[FourierTransform[f@t, t, s, FourierParameters->{1, 1}],
s, t, FourierParameters -> {1, 1}]
will return the input, not f[t].
Let's have some tests.
It can of course handle your toy example, back and forth:
f = PDF@NormalDistribution[μ, σ];
Simplify[BilateralLaplaceTransform[f@o, o, -t], σ > 0]
Simplify[InverseBilateralLaplaceTransform[% /. t -> -t, t, o], σ > 0]

And what's more important is, it handles DE now!:
teqn = BilateralLaplaceTransform[D[u[x, t], t] == D[u[x, t], x, x], t, s]
With[{f = FourierTransform, d = Derivative, h = HoldPattern},
teqn /. {h@f[u[a_, b_], , _] -> u[a], h@f[d[c, e_][u][a_, b_], _, _] -> d[c][u][a]}]
InverseBilateralLaplaceTransform[teqn, s, t]
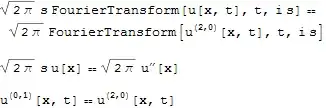
##Old Answer##
Not a complete answer. According to the wikipedia of two-sided Laplace transform, the relationship between two-sided Laplace transform and one-sided Laplace transform is:
$$\mathcal{B}\{f(t)\}(s) = \mathcal{L}\{f(t)\}(s) + \mathcal{L}\{f(-t)\}(-s)$$
If I understand the above formula correctly, it can be implemented as the following:
BilateralLaplaceTransform[f_, t_, s_] :=
LaplaceTransform[f[t], t, s] + LaplaceTransform[f[-t], t, -s]
Notice that here f should be a functional relationship e.g. a pure function. It does handle your specific example:
f = PDF@NormalDistribution[μ, σ]
FullSimplify[BilateralLaplaceTransform[f, o, -t], σ > 0]
E^(1/2 t (2 μ + t σ^2))
But the troublesome part is, you mentioned that you want to solve a ODE i.e. you want to make use of the differentiation property of the transform, but currently my BilateralLaplaceTransform can not handle it properly:
BilateralLaplaceTransform[g', t, s]
-2 g[0] - s LaplaceTransform[g[-t], t, -s] + s LaplaceTransform[g[t], t, s]
The result is even incorrect, I'm not sure.
BTW, if you're just trying to solve a ODE from $-\infty$ to $+\infty$, you may want to read this and this post about Fourier transform.


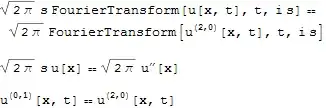
FourierParametersoption if the normalization constant is not to your liking. – J. M.'s missing motivation May 12 '15 at 13:52InverseFourierTransformdoesn't know 囧:http://i.stack.imgur.com/PGcPh.png – xzczd May 13 '15 at 01:19