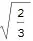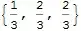20

I am trying to compute the shortest distance between a point and a triangle in 3D

distance[point_, {p1_, p2_, p3_}] := Module[{p, s, t, sol},
  p = s*p1 + (1 - s)*(t*p2 + (1 - t)*p3);
  MinValue[{(point - p).(point - p),
   0 <= s <= 1, 0 <= t <= 1}, {s, t}]];

but it seems to be quite slow, is there any way to make it faster?

RunnyKine
  • 33,088
  • 3
  • 109
  • 176
tintin
  • 739
  • 3
  • 15
  • As I unfortunately do not know your intended application this may not work for your purposes, however I would suggest to redefine your triangle as a hyperplane and use LeastSquares[]. This is as a built in function much faster compared to the iteration you have designed here. – Sander May 27 '14 at 03:20

1 Answers1

32

Well, you can use the undocumented RegionDistance which does exactly this as follows: (This answer, as written, only works for V9 as noted by Oska, for V10 see update below)

here is a triangle in 3D

region = Polygon[{{0, 0, 0}, {1, 0, 0}, {0, 1, 1}}];

Graphics3D[region]

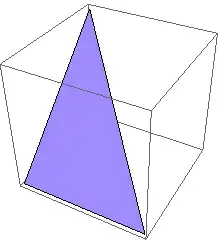
Mathematica graphics

Now suppose you want to find the shortest distance from the point {1, 1, 1} in 3D to this triangle just do the following:

Load the Region context

Graphics`Region`RegionInit[];

Then

RegionDistance[region, {1, 1, 1}]

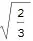
Mathematica graphics

As a bonus, you can get the exact point on the triangle that is closest to the given point as follows:

RegionNearest[region, {1, 1, 1}]

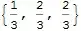
Mathematica graphics

Visualize it

Graphics3D[{region, Darker@Green, PointSize[0.03], Point[{1, 1, 1}], 
  Red, PointSize[0.03], Point[{1/3, 2/3, 2/3}]}]

Mathematica graphics

Update for Version 10

The above undocumented functions used in this answer now works out of the box in V10 so no need to load the Region context as I did above. Otherwise everything works as is. Also, now you can use the new Triangle function in place of Polygon above.

Community
  • 1
RunnyKine
  • 33,088
  • 3
  • 109
  • 176