I know Mathematica is really powerful when it comes to functional operations like applying a list of tasks to a list of variables. Sometimes I feel like it isn't the most powerful tool when it comes to looking for a number in a large range. But that's what I'd like to use it for regardless. I can always use a While loop, but I'm not sure that is the most effective way of doing it. So I'm looking for a more elegant/effective way of doing this. Let me give you an example:
Question: Find the smallest positive integer whose sum of its digits squared is greater than 100.
My rather sloppy solution:
myInt = 0;
mySum = 0;
SumLimit = 100;
While[mySum < SumLimit,
myDigits = IntegerDigits[myInt];
mySum = Total[#^2 & /@ myDigits];
myInt = myInt + 1;
]
myInt - 1
And the answer is 59.
But as you can clearly see, this method is quite slow. If I said 1000 instead of 100, it would take quite a long time to find. There are obviously better ways to solve this problem than brute force, but I'd basically like to have a more elegant implementation of the brute force method.
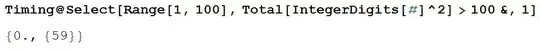
While[Total@(IntegerDigits[++myInt]^2) < SumLimit]` – george2079 Jun 18 '14 at 20:35Compileand that just shows that it's implementation and documentation are terrible @Kuba. – RunnyKine Jun 18 '14 at 21:03