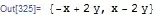3

I have the following problem. Consider expression

f=Sqrt[(x-2y)^2]

There is an obvious ambiguity in the definition of f related to multivaluedness of the square root. Two possible interpretations for f are $x-2y$ or $2y-x$.

My needs require to work with power series expansions of expressions like f. When asked to perform a series expansion Mathematica automatically chooses a branch

Series[f, {x, 0, 1}, {y, 0, 1}] // Normal

(* -x + 2 y *)

I'm OK with that since I can adjust the sign of the square root manually and use -f instead of f if needed. The problem is that Mathematica is not consistent in her choice. For example, evaluate 

Series[f, {y, 0, 1}, {x, 0, 1}] // Normal

(* x - 2 y *)

now it's the other branch!

In a real task I have a quite complicated function depending on many parameters under the square root. When I work with its series expansions naively, as described above, things just go wrong. How can the problem be handled?

Any help is appreciated!

J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574
Weather Report
  • 535
  • 2
  • 15
  • not clear what you are after. Do you want both expressions, or do you want a single result that is somehow consistent to you? maybe an example of where this is a real issue would help – george2079 Jun 23 '14 at 13:09
  • why is mathematica a "her" when it's doing something that is not consistent...is what I wonder – cherzieandkressy Nov 09 '21 at 13:42

3 Answers3

5

I just saw this trick here http://www.math.ubc.ca/~feldman/m200/taylor2dSlides.pdf, page 2 and decided to try it on this problem. Another reference that describes this method is here https://math.stackexchange.com/questions/67896/multivariate-taylor-series-derivation-2d

The idea is to convert multiple Taylor series in $x,y$ to one variable $t$ as follows

   f[t_] := Sqrt[((x0 + t x) - 2 (y0 + t y))^2];

Now $f(t)$ can be expanded in Taylor as single variable to avoid the issue at hand.

The trick is to set t->1 afterwords and then take the limit of x0->0 and y0->0 since we are expanding around these which are zeros. Doing so, gives both solutions. Now depending on if we take the limit of x0->0 or y0->0 we get one of the solutions returned by Mathematica's Series!

But this way, you obtain both limits and then you can decide which one to use. 

Clear[x0, t, x, y0, y]
f[t_] := Sqrt[((x0 + t x) - 2 (y0 + t y))^2];
r = Normal[Series[f[t], {t, 0, 1}]] /. t -> 1;
r = Simplify@Expand@ComplexExpand[%];
r = Limit[r, {x0 -> 0, y0 -> 0}]; %had to take limit 2 times to do it!
Limit[r, {y0 -> 0, x0 -> 0}]

Mathematica graphics

Compare the above to 

f[x_, y_] := Sqrt[(x - 2 y)^2];
Normal[Series[f[x, y], {x, 0, 1}, {y, 0, 1}]] // Normal
(*-x + 2 y*)
Normal[Series[f[x, y], {y, 0, 1}, {x, 0, 1}]] // Normal
(* x - 2 y *)

So, the single variable trick gives you both solutions. It seems Series takes the limit based on the order of the variables. Not sure about that. I can't explain exactly why Series did that, but I do not think it is a branch cut issue as you can see.

Community
  • 1
Nasser
  • 143,286
  • 11
  • 154
  • 359
2

While I'm not sure how one might expect Mathematica to pick the "right" result, if getting the possible results gets you part way there. a simpler way to do this is:

mySeries[f_, p_] := DeleteDuplicates@(Normal@Series[f, Sequence @@ #] & /@ Permutations[p])

f = Sqrt[(x - 2 y)^2]
p = {{x, 0, 1}, {y, 0, 1}}
mySeries[f, p]

(* {-x + 2 y, x - 2 y} *)
ciao
  • 25,774
  • 2
  • 58
  • 139
1

In M11.3+ giving Series an Assumptions option returns the outputs you want:

Series[f, {x,0,1}, {y,0,1}, Assumptions->x<2y] //Normal
Series[f, {y,0,1}, {x,0,1}, Assumptions->x<2y] //Normal

-x + 2 y

-x + 2 y

And with the opposite assumption:

Series[f, {x,0,1}, {y,0,1}, Assumptions->x>2y] //Normal
Series[f, {y,0,1}, {x,0,1}, Assumptions->x>2y] //Normal

x - 2 y

x - 2 y

Carl Woll
  • 130,679
  • 6
  • 243
  • 355