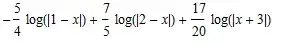3

Evaluating

$$\int \frac{x^2-x+5}{(x-2) (x-1) (x+3)} \, dx$$

Version 9.0.1 gives the following answer

$$\frac{1}{4} (-5) \log (1-x)+\frac{7}{5} \log (2-x)+\frac{17}{20} \log (x+3)$$

It seems to me that the correct answer should be

$$ \frac{1}{4} (-5) \log \color{Red}{|x-1|}+\frac{7}{5} \log \color{Red}{|x-2|}+\frac{17}{20} \log \color{Red}{|x+3|} + C $$

Am I missing something? Is there a fix?

Edit:

Integrate[(x^2 - x + 5)/((x - 2)*(x - 1)*(x + 3)), x]
Clif
  • 697
  • 4
  • 12
  • 6
    Please post Mathematica code to go with your problem. First Mathematica always returns an antiderivative, not the general antiderivative. Second, in terms of complex functions, Mathematica's answer agrees with the "correct" answer up to a (complex) constant. (Technically, the "correct" answer can have different constants over each interval of its natural domain, so Mma's answer agrees up to a constant over each interval.) – Michael E2 Jul 01 '14 at 00:57
  • 2
    Related question – Jens Jul 01 '14 at 01:03
  • 1
    You can see the constant by calling WolframAlpha: WolframAlpha["Integrate (x^2-x+5)/((x-2) (x-1) (x+3)) dx", {{"IndefiniteIntegral", 1}, "Content"}] – Bob Hanlon Jul 01 '14 at 02:27
  • Thanks to all for the comments and answers. I am choosing Junho's answer and would hope that in future releases of "Wolfram" that the absolute value is shown where it is needed. – Clif Jul 01 '14 at 13:56
  • 4
    The absolute value is not going to appear in the antiderivative for the simple reason that it is not correct (it's not an analytic function whereas antiderivatives in this example are analytic). – Daniel Lichtblau Jul 01 '14 at 16:16

3 Answers3

9

The answer is emphatically - no, the correct integral should not involve absolute values.

To fully understand what's going on, it should suffice to examine the simpler situation

Integrate[1/z, z]
(*Out: Log[z] *)

Presumably, the expected answer is, as we learn in calculus 1: $$\int \frac{1}{z} \, dz = \ln\left|z\right|+c.$$

As Junho points out in his answer, however, Mathematica generally assumes that everything is complex and, in the complex context, the above anti-differentiation formula is simply not correct. In fact, $F(z)=\ln\left|z\right|$ is not even differentiable so it certainly can't be the anti-derivative of $1/z$ or anything else. A quick way to see this with Mathematica is to compute:

D[Log[Abs[z]], z] 
(*Out: Abs'[z]/Abs[z] *)

Well, that's not 1/z. In fact, it's complete nonsense, as the absolute value function is nowhere differentiable as a complex function.

The most elementary way to see what's going on mathematically is via the Cauchy-Riemann equations, i.e. if we separate a complex function into its real and imaginary parts, $$f(z)=f(x+iy)=u(x,y)+i\,v(x,y),$$ we have $$u_x = v_y \; \text{ and } \; u_y=-v_x.$$

Examining $f(z)=1/z$, for example,

ComplexExpand[1/(x + I*y)]
(*Out: x/(x^2 + y^2) - (I y)/(x^2 + y^2) *)

and 

Simplify[D[x/(x^2 + y^2), x] == D[-y/(x^2 + y^2), y]]
(*Out: True *)

Now, suppose we apply this to the purported anti-derivative $\ln\left|z\right|$. Since this function is purely real valued, it's expansion into real and imaginary parts is $$\ln\left|z\right| = \ln\left|x+i\,y\right| = u(x,y)+i\,v(x,y) = \ln\left(\sqrt{x^2+y^2}\right) + 0\,i.$$ Thus $$u(x,y) = \ln\left(\sqrt{x^2+y^2}\right) \; \text{ and } \; v(x,y) = 0.$$ But, then, the Cauchy-Riemann equations are not satisfied!

Now, let's examine Mathematica's choice. Again:

Integrate[1/z, z]
(*Out: Log[z] *)

where Log is base E. It appears to work out, as far as the derivative is concerned:

D[Log[z], z] 
(*Out: 1/z *)

Let's see if Log[z] satisfies the Cauchy-Riemann equations. We'll start with a ComplexExpand:

antiDerivative = ComplexExpand[Log[x + I*y]] 
(*Out: I*Arg[x + I*y] + Log[x^2 + y^2]/2 *)

Well, the Arg function makes things a bit tricky here since, like Abs it's not differentiable. We can replace Arg[x+I*y] with ArcTan[y/x], though to obtain an analytic expression. Then

Simplify[D[Log[x^2 + y^2]/2, x] == D[ArcTan[y/x], y]] 
(*Out: True *)
Mark McClure
  • 32,469
  • 3
  • 103
  • 161
  • Thank you very much, I did not start out to ask a math question per se, but have learned a lot of math in the process (even if it is contrary to Calc 1). Guess that the only thing I now need to find out is if there is a way to return to Mathematica's default definition of Integrate – Clif Jul 01 '14 at 17:17
  • 4
    To add ever so little, one can use log(sqrt(x^2)) as a correct antiderivative, and then make the observation that, over the reals, it is equivalent to log|x|. But that equivalence does not hold elsewhere in the complex plane, hence log|x| is not a correct antiderivative. – Daniel Lichtblau Jul 01 '14 at 17:20
6

The result Mathematica returns may not be completely general but it is strictly true.

Reduce[(x^2 - x + 5)/((x - 2)*(x - 1)*(x + 3)) == 
         D[(-5 Log[1 - x]/4 + 7 Log[2 - x]/5 + 17 Log[3 + x]/20), x]]

True
m_goldberg
  • 107,779
  • 16
  • 103
  • 257
1

Since Mathematica generally assumes that everything is complex, I'm not sure if there is a simple way to make it return the result you want. 

Unprotect[Integrate];
Integrate[f_, x_Symbol] := 
 Block[{used = True}, 
   Simplify[Integrate[f, x] /. Log[expr_] :> Log[Abs[expr]], 
    Element[x, Reals]]
   ] /; ! TrueQ[used]
Protect[Integrate];

Integrate[(x^2 - x + 5)/((x - 2)*(x - 1)*(x + 3)), x] // Expand // TraditionalForm

enter image description here

Junho Lee
  • 5,155
  • 1
  • 15
  • 33