9

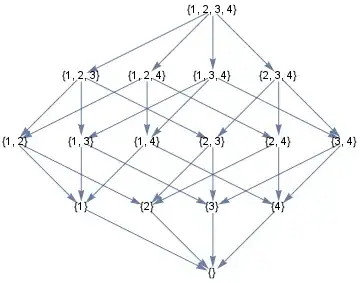
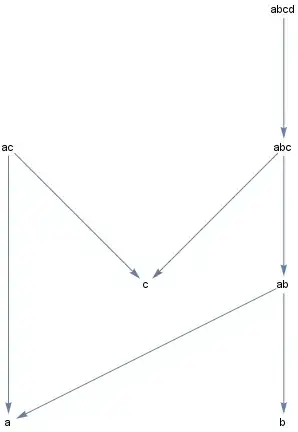
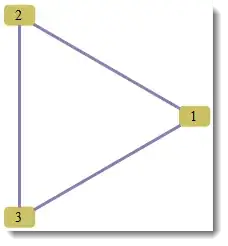
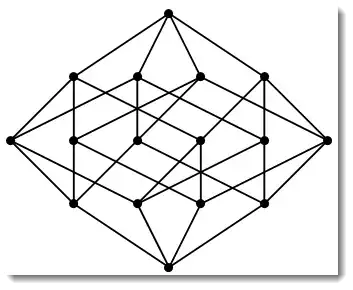
I'm looking for a way to create a Hasse Diagram from a given partial order binary relation. The relation will be given explicitly, for example: Hasse[{{1,2},{2,3},{1,3}}], and the output will be the corresponding graph.

I've googled for a solution, and I did find some solution, but I didn't get how to use it.. here's what I found.

If there is a way to generate a Hasse diagram for a conditional partial order set, and for a non-finite relation (of course, for this case I'm only interested in an approximate diagram), I would be happy to hear about it too.

user64494
  • 26,149
  • 4
  • 27
  • 56
rboy
  • 191
  • 1
  • 3
  • Which part of the code you referred to didn't you understand? – Sjoerd C. de Vries May 08 '12 at 21:16
  • Well, I didn't understand how to use it for my purpose. meaning, how do I define the relation explicitly (like the example above). It seems it only allows me to draw a graph only for conditional relation.. well I could define the relation with condition, but isn't there something simpler? and one more problem, I played with it a little, and I couldnt find a way to change the font size of the labels.. I want to copy the graph to word, and the labels must be readable, and not that small. – rboy May 08 '12 at 21:42
  • If you specify the relations between the nodes explicitly isn't it just a graph then? – Sjoerd C. de Vries May 08 '12 at 22:04
  • I'm sorry, I'm new to Mathematica. Anything that would look like a graph of my description would be fine. I don't need to do calculations on it. But I have a lot of graphs to draw, and I hoped there is a dedicated function for my needs. if you have another solution, feel free to let me know.. but keep in mind that I'm new to Mathematica, so I'm not familiar with lots of the basics methods of the program. – rboy May 08 '12 at 22:32
  • Welcome to Mathematica Stack Exchange RB14, I will post an answer shortly (well...after lunch :-)) – magma May 13 '12 at 10:59
  • @magma that's quite a looong lunch break you have ;) – rm -rf Jul 24 '12 at 14:54
  • @R.M Indeed ! The point is that Hasse diagrams are supported by the Combinatorica package, but you need first to convert the Graph information in a suitable form, acceptable to the Combinatorica functions. Someone on this forum probably knows how to do it, without having to go through the whole documentation – magma Jul 24 '12 at 18:13

2 Answers2

5

In versions 10+, we can compose TransitiveReductionGraph and RelationGraph to get a Hasse diagram function with takes the same arguments and options as RelationGraph: 

ClearAll[hasseF]
hasseF = TransitiveReductionGraph @* RelationGraph

Examples:

hasseF[SubsetQ, Subsets[Range[4]], VertexShapeFunction -> "Name"]

enter image description here

substringQ[s1_, s2_] := UnsameQ[s1 , s2] && StringMatchQ[s1, ___ ~~ s2 ~~ ___]

hasseF[substringQ, {"a", "b", "c","ab", "ac","abc", "abcd"},
   VertexShapeFunction -> "Name"]

enter image description here

kglr
  • 394,356
  • 18
  • 477
  • 896
3

I think what you want is actually very simple (also noted by @SjoerdC.deVries in his comment):

Graph[{1 -> 2, 2 -> 3, 3 -> 1}, DirectedEdges -> False, GraphStyle -> "DiagramGold"]

enter image description here

If, on other hand, you'd like to explore full featured Hasse Diagrams, the code you linked to is a good start. Also Demonstrations Project has a few relevant examples - it is always a good idea to search there.

Digging deeper, Mathematica built in Combinatorica package has HasseDiagram package. Take a look at this example from Documentation requires

<< Combinatorica`

ShowGraph[HasseDiagram[MakeGraph[Subsets[4], #2 \[Intersection] #1 === #1 && #1 != #2 &]]]

enter image description here

For even deeper functionality you may want to contact authors of this paper:

"A Mathematica package to cope with partially ordered sets", P. Codara

or get this book:

"Computational Discrete Mathematics: Combinatorics and Graph Theory with Mathematica", Sriram Pemmaraju, Steven Skiena

Vitaliy Kaurov
  • 73,078
  • 9
  • 204
  • 355
  • If the asker wants a true Hasse Diagram, surely he wants an automatic way to compute the transitive reduction of the directed graph generated by the binary relation. The arrows should be directed, I think, and the arrow between 1 and 3 shouldn't be there. – JOwen Jul 25 '12 at 00:11
  • @JOwen Do you know why standard representation then is not directed? http://alturl.com/jribp – Vitaliy Kaurov Jul 25 '12 at 00:31
  • I'm not certain but I think there is directional information in the edges. It says in the link you posted that one should draw "a line segment or curve that goes upward [italicized in the original] from x to y whenever y covers x (that is, whenever x < y and there is no z such that x < z < y)" – JOwen Jul 25 '12 at 00:48