Hasse Diagrams in Mathematica using an arbitrary relation

Question

As a kludge to draw Hasse diagrams for an assignment, I wrote(based on this):

chars = {"a", "b", "c", "d", "e", "f"}; 
nums = Association["a" -> 1, "b" -> 2, "c" -> 3, "d" -> 4, "e" -> 5,"f" -> 6]; 
edges = EdgeList[
   AdjacencyGraph[{{1, 0, 1, 1, 0, 0}, {0, 1, 0, 1, 0, 0}, 
           {0, 0, 1, 0, 0, 0}, {0, 0, 0, 1, 0, 0}, {1, 1, 1, 1, 1, 0}, 
           {0, 1, 0, 1, 0, 1}}]];
pOrder[x_, y_] := MemberQ[edges, DirectedEdge[nums[x], nums[y]]]; 
g = MakeGraph[chars, pOrder, VertexLabel -> True]; 
h = HasseDiagram[g]; 
ShowGraph[h, VertexStyle -> PointSize[0.1], VertexLabelColor -> White, 
   VertexLabelPosition -> {0.025, 0}, BaseStyle -> {FontSize -> 18}]

I have read Is it possible to generate a Hasse Diagram for a defined relation? but the only answer provided was deeply insufficient for me, since contacting the authors or buying the book would take a long time or money. So my question is: Is there a better way to do this? More precisely: Does mathematica have some object to draw a Hasse Diagram from DirectedEdges or adjacency matrices, preferrably working with labels directly? Optionally, is there a way to relate "a" to 1, "b" to 2 and so on without doing it explicitly?

Dr. belisarius · Accepted Answer · 2014-10-03T07:33:34.990

6

I'm not sure if I understand your question. I'm trying to answer:

Does mathematica have some object to draw a Hasse Diagram from DirectedEdges or adjacency matrices

So, let's draw a Hasse Diagram starting from its adjacency matrix:

<< Combinatorica`;
am = {{1, 1, 1, 1, 1, 1, 1}, {0, 1, 1, 0, 1, 1, 1}, {0, 0, 1, 0, 1, 0, 0}, 
      {0, 0, 0, 1, 0, 1, 0}, {0, 0, 0, 0, 1, 0, 0}, {0, 0, 0, 0, 0, 1, 0}, {0, 0, 0, 0, 0, 0, 1}};
g = FromAdjacencyMatrix[am, Type -> Directed];
h = HasseDiagram[SetVertexLabels[g, CharacterRange["a", "g"]]];
ShowGraph[h, BaseStyle -> {FontSize -> 18}]

Mathematica graphics

edited Oct 03 '14 at 07:33

answered Sep 29 '14 at 11:29

Dr. belisarius

115,881
13
203
453

This was just was I was looking for! It was just plain odd to use a binary function as a proxy to make things work(and relabeling each vertex "manually"). – chubakueno Sep 29 '14 at 16:45
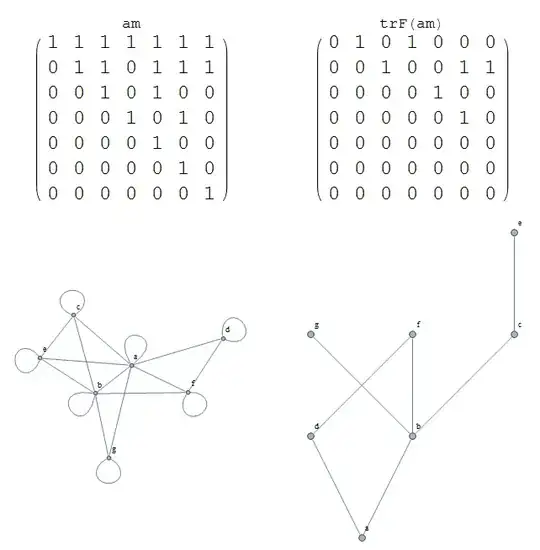
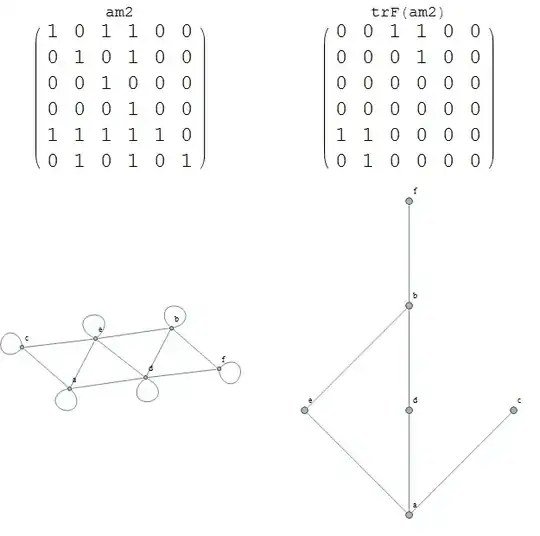
I wonder how HasseDiagram chooses to arrange the vertices. The placement of vertex a in this diagram is puzzling. (Good answer though, of course. I'm just thinking out loud.) – Kellen Myers Sep 29 '14 at 19:32
1

@KellenMyers Take a look at C:\Program Files\Wolfram Research\Mathematica\10.0\AddOns\Packages\Combinatorica (or something like that) .A stripoff of Combinatorica.m shows that it just uses the vertexes in their raw order and puts them left to right. The function even has an undocumented parameter fak that makes the hasse diagram look pyramid-like(coarsely) – chubakueno Oct 01 '14 at 20:38
@belisarius I just noted that the range should be ["a","g"] – chubakueno Oct 03 '14 at 02:12
@chubakueno Gracias! Cuando veas un error así no dudes en editar la respuesta y corregirlo. Saludos – Dr. belisarius Oct 03 '14 at 07:32
Entendido! Saludos también. – chubakueno Oct 05 '14 at 06:34

kglr · Answer 2 · 2018-01-17T07:59:14.797

The key function used in Combinatorica`HasseDiagram is the transitive reduction function TR.

 TR = Compile[{{closure, _Integer, 2}},
   Module[{reduction = closure, n = Length[closure], i, j, k},
     Do[If[reduction[[i, j]] != 0 && reduction[[j, k]] != 0 &&
      reduction[[i, k]] != 0 && (i != j) && (j != k) && (i != k), reduction[[i, k]] = 0],
    {i, n}, {j, n}, {k, n}]; 
    reduction]]

You can use the Combinatorica function TR on your adjacency matrix to get its transitive reduction and use the resulting matrix with AdjacencyGraph.

The function trF below is an alternative implementation of TR.

ClearAll[trF];
trF = Module[{r = #, m = Length@#},
  Table[r[[i, k]] = r[[i, k]] (1 - Times @@ Unitize[{r[[i, j]], r[[j, k]], r[[i, k]],
   i - j, j - k, i - k}]), {i, m}, {j, m}, {k, m}]; r] &;

Using the example matrix in belisarius's answer:

am = {{1, 1, 1, 1, 1, 1, 1}, {0, 1, 1, 0, 1, 1, 1}, {0, 0, 1, 0, 1, 0,
     0}, {0, 0, 0, 1, 0, 1, 0}, {0, 0, 0, 0, 1, 0, 0}, {0, 0, 0, 0, 0,
     1, 0}, {0, 0, 0, 0, 0, 0, 1}};

tram0 = TR[am - IdentityMatrix[Length@am]];
tram = trF[am - IdentityMatrix[Length@am]];
tram == tram0;
(* True *)

The Hasse Diagram can be obtained using AdjacencyGraph[tram]:

options = {VertexLabels -> "Name", ImagePadding -> 20, 
  DirectedEdges -> False, ImageSize -> 300};

agam = AdjacencyGraph[CharacterRange["a", "g"], am, options];
agtram = AdjacencyGraph[CharacterRange["a", "g"], tram, options, 
   GraphLayout -> {"LayeredEmbedding", "RootVertex" -> "a", "Orientation" -> Bottom}];

{{"am", "trF[am]"}, {am // MatrixForm, tram2 // MatrixForm}, {agam, agtram}} // Grid

enter image description here

OP's example:

am2 = {{1, 0, 1, 1, 0, 0}, {0, 1, 0, 1, 0, 0}, {0, 0, 1, 0, 0, 0}, 
       {0, 0, 0, 1, 0, 0}, {1, 1, 1, 1, 1, 0}, {0, 1, 0, 1, 0, 1}};
tram2 = trF[am2 - IdentityMatrix[Length@am2]];

agam2 = AdjacencyGraph[CharacterRange["a", "f"], am2,  options];
agtram2 = AdjacencyGraph[CharacterRange["a", "f"], tram2, options,
   GraphLayout -> {"LayeredEmbedding", "RootVertex" -> "a", "Orientation" -> Bottom}];

{{"am2", "trF(am2)"}, {am2 // MatrixForm, tram2 // MatrixForm }, {agam2, agtram2}} // Grid

enter image description here

Thank you for providing an insight to mathematica's inner workings, now I know packages are actually an analyzable .m file :) — chubakueno, Oct 01 '14 at 20:25

Hasse Diagrams in Mathematica using an arbitrary relation

2 Answers2

Linked