5

Is there a command to insert an item into a list such that they form pairs? In other words to take 

InsertObject[{a,b,c},d]

which will output

{{a,d},{b,d},{c,d}}    ?

This would be equivalent to the function,

Table[{{a,b,c}[[i]],d},{i,1,3}]

This way works just fine, but it doesn't seem to be the "Mathematica way" of doing things. Is there a built in command this?

JeffDror
  • 1,880
  • 1
  • 13
  • 29

3 Answers3

13

Few more alternatives:

{#, d} & /@ {a, b, c}
Tuples[{{a, b, c}, {d}}]
Join[{#}, {d}] & /@ {a, b, c}
Table[{i, d}, {i, {a, b, c}}]
Append[{#}, d] & /@ {a, b, c}
Prepend[{d}, #] & /@ {a, b, c}
Riffle[{#}, {d}] & /@ {a, b, c}
Distribute[{{a, b, c}, d}, List]
Insert[{#}, d, -1] & /@ {a, b, c}
Replace[{a, b, c}, x_ :> {x, d}, 1]
PadRight[List /@ {a, b, c}, {3, 2}, d]
ArrayPad[List /@ {a, b, c}, {0, {0, 1}}, d]
Partition[Riffle[{a, b, c}, d, {2, -1, 2}], 2]
Transpose[{{a, b, c}, ConstantArray[d, {3}]}]
Transpose[{{a, b, c}, Table[d, {3}]}]

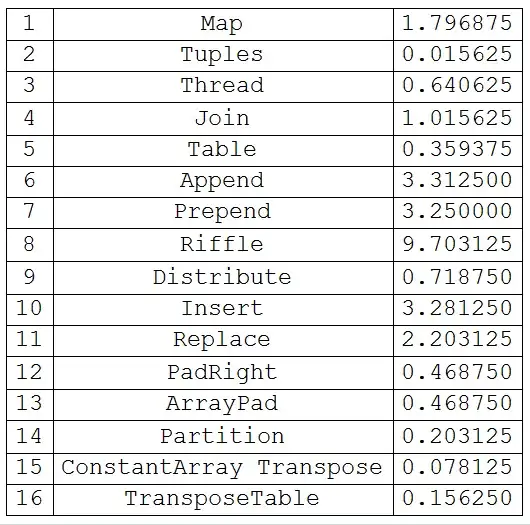
Timings:

f1[lst_, elem_] := Map[{#, elem} &, lst]
f2[lst_, elem_] := Tuples[{lst, {elem}}]
f3[lst_, elem_] := Thread[{lst, elem}]
f4[lst_, elem_] := Join[{#}, {elem}] & /@ lst
f5[lst_, elem_] := Table[{i, elem}, {i, lst}]
f6[lst_, elem_] := Append[{#}, elem] & /@ lst
f7[lst_, elem_] := Prepend[{elem}, #] & /@ lst
f8[lst_, elem_] := Riffle[{#}, {elem}] & /@ lst
f9[lst_, elem_] := Distribute[{lst, elem}, List]
f10[lst_, elem_] := Insert[{#}, elem, -1] & /@ lst
f11[lst_, elem_] := Replace[lst, x_ :> {x, elem}, 1]
f12[lst_, elem_] := PadRight[List /@ lst, {Length@lst, 2}, elem]
f13[lst_, elem_] := ArrayPad[List /@ lst, {0, {0, 1}}, elem]
f14[lst_, elem_] := Partition[Riffle[lst, elem, {2, -1, 2}], 2]
f15[lst_, elem_] := Transpose[{lst, ConstantArray[elem, {Length@lst}]}]
f16[lst_, elem_] := Transpose[{lst, Table[elem, {Length@lst}]}]

funcs = {f1, f2, f3, f4, f5, f6, f7, f8, f9, f10, f11, f12, f13, f14,  f15, f16};
labels = ToString /@ {Map, Tuples, Thread, Join, Table, Append,
                    Prepend, Riffle, Distribute, Insert, Replace, PadRight, ArrayPad, 
                    Partition, TransposeConstantArray, TransposeTable};
res = ConstantArray[0, {16}];

testdata = RandomInteger[10, {10000000}];
Grid[Table[{i, labels[[i]],  First@Timing[res[[i]] = funcs[[i]][testdata, 20];]},
            {i,  Range[16]}], 
     Dividers -> All]

enter image description here

And@@(res[[1]] == # & /@ Rest[res])
(* True *)
kglr
  • 394,356
  • 18
  • 477
  • 896
  • @eldo, thanks for the vote. I am sure there is at least half a dozen more ways -- e.g. Through[{a, b, c}[d]] /. x_[y_] :> {x, y} or {a, b, c} d /. Times -> List :) – kglr Jul 15 '14 at 03:07
  • +1 I lol'd at wall of ways and the readers digest large print edition benchmark chart ;-) – ciao Jul 15 '14 at 04:37
  • @rasher, thank you -- fontsize does indeed look like readers digest style even for my generation:) Still expecting some BitXor magic from you though to update the chart:) – kglr Jul 15 '14 at 05:39
  • They say imitation is the sincerest form of flattery. I'm feeling flattered. :^) – Mr.Wizard Jul 15 '14 at 08:29
  • @Mr.W indeed! As we have all learned to expect, a totally unexpected idiom is due soon now that this question got your attention :) – kglr Jul 15 '14 at 09:00
  • @kguler Sorry to disappoint but I won't be spending time on this. I think this class of problem has been well covered every before your omnibus answer, and now few stones are left unturned. I've got lots of other things to learn about in the v7 -> v10 transition. – Mr.Wizard Jul 15 '14 at 09:03
  • @Mr.W, btw, congratulations on the v10 license! – kglr Jul 15 '14 at 09:07
8

Indeed there is:

Thread[List[{a, b, c}, d]]
(* {{a, d}, {b, d}, {c, d}} *)

or if you like Thread[{{a, b, c}, d}] but I thought the first version shows more which function is threaded.

halirutan
  • 112,764
  • 7
  • 263
  • 474
2

Thanks to kguler.

Here are few more.

list = {a, b, c};
{list[[#]], d} & /@ Range[3]
{Pick[list, #, 1][[1]], d} & /@ IdentityMatrix[3]
{Extract[list, #], d} & /@ Range[3]
{Take[list, {#}][[1]], d} & /@ Range[3]
Flatten@ReplacePart[{#}, 1 -> {#, d}] & /@ list
Array[{list[[#]], d} &, 3]
{#, d} & @@@ (Transpose@{list})
Basheer Algohi
  • 19,917
  • 1
  • 31
  • 78