Zero-order interpolation not going fully around

Question

Connected to this question, I want to do a zero-order interpolation of a bunch of datapoints which is periodic. The code I use is as follows:

dataSource = {{-0.225, 0.250}, {0.000, 0.250}, {0.225, 0.250}, {0.225,
0.250}, {0.296, 0.231}, {0.367, 0.108}, {0.367, 0.107}, {0.354, 
0.048}, {0.341, 0.025}, {0.341, 
0.025}, {0.265, -0.082}, {0.189, -0.190}, {0.189, -0.190}, {0.131, 
-0.238}, {0.072, -0.250}, {0.072, -0.250}, {0.000, -0.250}, {-0.072, 
-0.250}, {-0.072, -0.250}, {-0.131, -0.238}, {-0.189, -0.190}, 
{-0.189, -0.190}, {-0.265, -0.082}, {-0.341, 0.025}, {-0.341, 
0.025}, {-0.354, 0.048}, {-0.367, 0.107}, {-0.367, 0.107}, {-0.296,
0.231}, {-0.225, 0.250}}

With[{ip = ListInterpolation[#, {{0, 1}}, InterpolationOrder -> 0, 
  PeriodicInterpolation -> True] & /@ Transpose[dataSource]}, 
fdata[t_] := Through[ip[t]]]

ParametricPlot[fdata[t], {t, 0, 1}, AspectRatio -> Automatic]

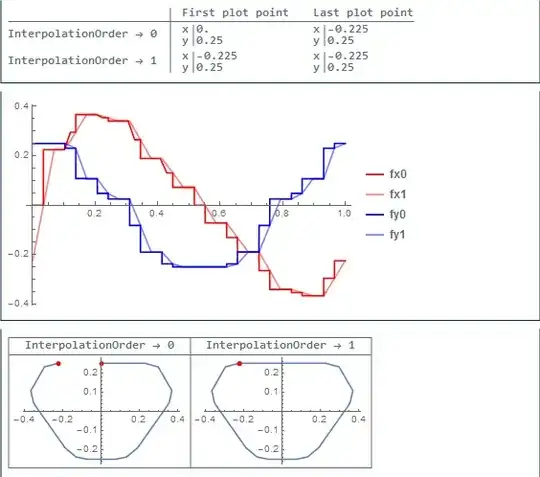
Which results in the following plot:

enter image description here

What I don't understand is why it doesn't draw the full contour? If I use InterpolationOrder -> 1 it does work, but I don't want to do that for other reasons. Can someone explain what is the problem that does not allow a periodic interpolation?

For clarification, the reason I don't want to use the first order interpolation is that it creates visual artifacts later on in the process:

enter image description here

As you can see the zero order extruded shape is nice and smooth, but with the gap from the cross-section. The first order extruded shape does not have this gap, but has a strange visual artifact.

The dataset for this last part is:

dataSource={{-0.225,0.250},{-0.192,0.250},{-0.160,0.250},{-0.128,0.250},{-0.096,0.250},{-0.064,0.250},{-0.032,0.250},{0.000,0.250},{0.032,0.250},{0.064,0.250},{0.096,0.250},{0.128,0.250},{0.160,0.250},{0.192,0.250},{0.225,0.250},{0.225,0.250},{0.230,0.250},{0.236,0.250},{0.242,0.249},{0.248,0.248},{0.254,0.247},{0.260,0.245},{0.266,0.244},{0.272,0.242},{0.278,0.240},{0.284,0.237},{0.290,0.234},{0.296,0.231},{0.302,0.227},{0.308,0.223},{0.314,0.219},{0.320,0.214},{0.326,0.208},{0.331,0.202},{0.337,0.195},{0.343,0.186},{0.349,0.176},{0.355,0.164},{0.361,0.148},{0.367,0.108},{0.367,0.107},{0.366,0.090},{0.365,0.083},{0.364,0.077},{0.363,0.072},{0.362,0.068},{0.361,0.065},{0.359,0.061},{0.358,0.058},{0.357,0.055},{0.356,0.053},{0.355,0.050},{0.354,0.048},{0.353,0.045},{0.352,0.043},{0.351,0.041},{0.350,0.039},{0.349,0.037},{0.347,0.035},{0.346,0.033},{0.345,0.032},{0.344,0.030},{0.343,0.028},{0.342,0.027},{0.341,0.025},{0.341,0.025},{0.330,0.010},{0.319,-0.006},{0.308,-0.021},{0.297,-0.036},{0.287,-0.052},{0.276,-0.067},{0.265,-0.082},{0.254,-0.098},{0.243,-0.113},{0.232,-0.128},{0.221,-0.144},{0.211,-0.159},{0.200,-0.174},{0.189,-0.190},{0.189,-0.190},{0.184,-0.196},{0.179,-0.202},{0.174,-0.207},{0.169,-0.212},{0.165,-0.216},{0.160,-0.220},{0.155,-0.224},{0.150,-0.227},{0.145,-0.230},{0.140,-0.233},{0.136,-0.235},{0.131,-0.238},{0.126,-0.240},{0.121,-0.242},{0.116,-0.243},{0.111,-0.245},{0.106,-0.246},{0.102,-0.247},{0.097,-0.248},{0.092,-0.249},{0.087,-0.249},{0.082,-0.250},{0.077,-0.250},{0.072,-0.250},{0.072,-0.250},{0.062,-0.250},{0.052,-0.250},{0.041,-0.250},{0.031,-0.250},{0.021,-0.250},{0.010,-0.250},{0.000,-0.250},{-0.010,-0.250},{-0.021,-0.250},{-0.031,-0.250},{-0.041,-0.250},{-0.052,-0.250},{-0.062,-0.250},{-0.072,-0.250},{-0.072,-0.250},{-0.077,-0.250},{-0.082,-0.250},{-0.087,-0.249},{-0.092,-0.249},{-0.097,-0.248},{-0.102,-0.247},{-0.106,-0.246},{-0.111,-0.245},{-0.116,-0.243},{-0.121,-0.242},{-0.126,-0.240},{-0.131,-0.238},{-0.136,-0.235},{-0.140,-0.233},{-0.145,-0.230},{-0.150,-0.227},{-0.155,-0.224},{-0.160,-0.220},{-0.165,-0.216},{-0.169,-0.212},{-0.174,-0.207},{-0.179,-0.202},{-0.184,-0.196},{-0.189,-0.190},{-0.189,-0.190},{-0.200,-0.174},{-0.211,-0.159},{-0.221,-0.144},{-0.232,-0.128},{-0.243,-0.113},{-0.254,-0.098},{-0.265,-0.082},{-0.276,-0.067},{-0.287,-0.052},{-0.297,-0.036},{-0.308,-0.021},{-0.319,-0.006},{-0.330,0.010},{-0.341,0.025},{-0.341,0.025},{-0.342,0.027},{-0.343,0.028},{-0.344,0.030},{-0.345,0.032},{-0.346,0.033},{-0.347,0.035},{-0.349,0.037},{-0.350,0.039},{-0.351,0.041},{-0.352,0.043},{-0.353,0.045},{-0.354,0.048},{-0.355,0.050},{-0.356,0.053},{-0.357,0.055},{-0.358,0.058},{-0.359,0.061},{-0.361,0.065},{-0.362,0.068},{-0.363,0.072},{-0.364,0.077},{-0.365,0.083},{-0.366,0.090},{-0.367,0.107},{-0.367,0.107},{-0.361,0.148},{-0.355,0.164},{-0.349,0.176},{-0.343,0.186},{-0.337,0.195},{-0.331,0.202},{-0.326,0.208},{-0.320,0.214},{-0.314,0.219},{-0.308,0.223},{-0.302,0.227},{-0.296,0.231},{-0.290,0.234},{-0.284,0.237},{-0.278,0.240},{-0.272,0.242},{-0.266,0.244},{-0.260,0.245},{-0.254,0.247},{-0.248,0.248},{-0.242,0.249},{-0.236,0.250},{-0.230,0.250},{-0.225,0.250}};

i dont understand why you get a plot at all. a zero order interpolation of 2d data it seems should give you discrete points (?). what do you get if you plot beyond the range 0-1? — george2079, Jul 26 '14 at 12:20
on furthe thought i suspect if you Plot[ftdata[t][[1]],{t,0,1}] this will begin to make sense. — george2079, Jul 26 '14 at 12:33
Why not use ListLinePlot[dataSource]? This gives the same plot you seem to want. After all, a zero-order interpolation means connecting the points with straight lines, and this is what ListLinePLot is designed for. — bill s, Jul 26 '14 at 12:55
sorry i cant actually run things here. my thought is the interpolation function is correct and you are seeing an artifact of the way plot handles discontinuous functions — george2079, Jul 26 '14 at 13:09
doesn't extending the plot range to eg 1.001 close it? I'm still at a loss as to why you dont just use the first order interpolation. — george2079, Jul 27 '14 at 19:49
I think you ought to keep first-order interpolation and ask a question about how to get rid of the visual artifacts. — , Jul 28 '14 at 05:43
I just see one dataset of length 30 posted in your answer. Where can I find the longer dataset you mentioned? — seismatica, Jul 28 '14 at 05:45
Are you sure the gap that you get for the new dataSource is from order 1? It seems like it may actually come from your order 0. Even so, changing your t to 1.001 solves the problem. — seismatica, Jul 28 '14 at 06:13
I tried your method with t = 1.001 and did not see any discontinuities in the graph (for both dataSources). My last comment was referring to you mentioning in your question that order 1 produces artifact, while in fact it doesn't (order 0 does). I suggest just using order 1 from now on. — seismatica, Jul 28 '14 at 07:03
Michiel and @seismatica I got an automatic flag for excessive comments. Please consider summarizing any important points and including them in the question, or an answer, then deleting some comments. — Mr.Wizard, Jul 28 '14 at 09:57

seismatica · Accepted Answer · 2014-07-28T11:06:14.237

Even though OP's problem is resolved in the question's comments, I hope to provide an explanation of why the gap appears in the parametric plot. Namely, I think InterpolationOrder -> 0 (specifically as an option to ListInterpolation*) is the culprit, as it starts with a jump/step from the first data point to the second data point.

Mathematica graphics

As a result, the interpolating function actually starts with the second point and ends with the last point, which means that this parametric plot does not start and end with the same point--hence the gap--even if the first and last points of the datset are identical. Try changing the second point of this dataset to match the last point (just use my code below) and you will see the gap disappear. Also observe in my plots that fx0 does not start and end at the same point (fy0 does, but only by coincidence).

This is in contrast to InterpolationOrder -> 1, whose interpolating function actually starts with the first point (and not second like the zero-order one does). Therefore, its parametric plot indeed closes whenever the first and last point of the dataset are the same (they do in this case).

dataSource = {{-0.225, 0.250}, {0.000, 0.250}, {0.225, 0.250}, {0.225,
     0.250}, {0.296, 0.231}, {0.367, 0.108}, {0.367, 0.107}, {0.354, 
    0.048}, {0.341, 0.025}, {0.341, 
    0.025}, {0.265, -0.082}, {0.189, -0.190}, {0.189, -0.190}, \
{0.131, -0.238}, {0.072, -0.250}, {0.072, -0.250}, {0.000, -0.250}, \
{-0.072, -0.250}, {-0.072, -0.250}, {-0.131, -0.238}, {-0.189, \
-0.190}, {-0.189, -0.190}, {-0.265, -0.082}, {-0.341, 0.025}, {-0.341,
     0.025}, {-0.354, 0.048}, {-0.367, 0.107}, {-0.367, 
    0.107}, {-0.296, 0.231}, {-0.225, 0.250}};

{fx0, fy0} = 
  ListInterpolation[#, {{0, 1}}, InterpolationOrder -> 0, 
     PeriodicInterpolation -> True] & /@ Transpose[dataSource];
{fx1, fy1} = 
  ListInterpolation[#, {{0, 1}}, InterpolationOrder -> 1, 
     PeriodicInterpolation -> True] & /@ Transpose[dataSource];

{{fx0[#], fy0[#]} & /@ {0, 1}, {fx1[#], fy1[#]} & /@ {0, 1}} // 
 TableForm[#, 
   TableHeadings -> {{"InterpolationOrder \[Rule] 0", 
      "InterpolationOrder \[Rule] 1"}, {"First plot point", 
      "Last plot point"}, {"x", "y"}}] &

Plot[{fx0[t], fx1[t], fy0[t], fy1[t]}, {t, 0, 1}, 
 PlotStyle -> {Red, {Red, Opacity[0.5]}, Blue, {Blue, Opacity[0.5]}}, 
 PlotLegends -> {"fx0", "fx1", "fy0", "fy1"}]

ParametricPlot[#, {t, 0, 1}, Mesh -> {{0, 1}}, 
    MeshStyle -> Directive[Red, AbsolutePointSize[5]]] & /@ {{fx0[t], 
    fy0[t]}, {fx1[t], fy1[t]}} // 
 Grid[{{"InterpolationOrder \[Rule] 0", 
     "InterpolationOrder \[Rule] 1"}, #}, Frame -> All] &

Mathematica graphics

*

It seems that InterpolationOrder -> 0 behaves this way for ListInterpolation (and Interpolation). It doesn't seem to behave this way as an option for ListLinePlot in the documentation for InterpolationOrder.

Mathematica graphics

Terrific summary of the problem and our discussion in the comments. Thanks again — Michiel, Jul 28 '14 at 11:01
good catch noting the inconsistency in the ListLinePlot and ListInterpolation implementations. Of course both strictly follow what the docs say: "yields a collection of flat regions, with steps at each data point " — george2079, Jul 28 '14 at 18:44

score 3 · Answer 2 · answered Jul 28 '14 at 19:10

End running the problem we can readily construct our own "zero order" interpolation function:

 myzero[t_] := (#[[1 + (Ceiling[Mod[t, 1]  (Length@# - 1) ] )]]) &@ dataSource

which gives your desired plot:

 ParametricPlot[myzero[t], {t, 0, 1}, AspectRatio -> Automatic]

same closed figure as your InterpolationOrder-> 1 result

note the function myzero is exactly the same as your fdata except that it returns the first point when the argument is exactly zero.

You might see if this fixes your extrusion result, though I concur with the comment that you should try to figure out whats wrong with the first order case.

score 2 · Answer 3 · edited Apr 13 '17 at 12:55

A similar thing happens in this question: How can the behavior of InterpolationOrder->0 be controlled?

As @seismatica has pointed out, ListInterpolation[data, InterpolationOrder -> 0][0] yields data[[2]], not data[[1]] as might be expected. Thus the range of the interpolating function, over the fundamental domain does not include the first point in data. This holds even if PeriodicInterpolation -> True is set -- unless one goes beyond the domain. For instance the following produce closed curves:

ParametricPlot[fdata[t], {t, 0 - $MachineEpsilon, 1}, AspectRatio -> Automatic]
ParametricPlot[fdata[t], {t, 0, 1 + $MachineEpsilon}, AspectRatio -> Automatic]

A more straightforward way to get a closed curve is

ParametricPlot[fdata[Mod[t, 1]], {t, 0, 1}, AspectRatio -> Automatic]

Mathematica graphics

Zero-order interpolation not going fully around

3 Answers3