Extrude 2D cross-section to 3D shape with shrinkfactor

Question

I would like to create a 3D shape from extrusion and scaling of a 2D contour. The 2D contour that I have looks like this:

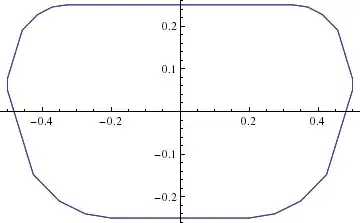
and it consists of a bunch of points (here plotted with ListPlot with Joined->True).

I have looked at a bunch of questions and answers here on Mathematica.SE, notably this one and this one, but I don't see how to apply those to my problem in any straightforward manner.

For the sake of a MWE I will switch to a circle from this point on:

xdata = Table[x, {x, -1, 1, 0.05}];
ydata = Table[Sqrt[1 - x^2], {x, -1, 1, 0.05}];
circData = {Transpose[{xdata, ydata}], Transpose[{xdata, -ydata}]};
ListPlot[circData, Joined -> True, AspectRatio -> Automatic]

The extruded shape that I would like to make then looks like this:

It is a shape consisting of slices of the contour with constant radius $r_0$ over some range let's say $-1 < z < 1$ and decrease in radius with $z$ at the tips according to $r(z)=r_0\sqrt{1-(z-1)^2}$ and $r(z)=r_0\sqrt{1-(z+1)^2}$ (depending on which tip).

My question is: how can I do this extrusion for the set of listdata that I have?

Just to be clear, to create the 3D shape for the circle I cheated and used the formula for a circle and a sphere like this:

p = Plot3D[{1 + Sqrt[1 - y^2 - x^2 ], -1 - 
     Sqrt[1 - y^2 - x^2 ]}, {x, -2, 2}, {y, -2, 2}, 
   PlotStyle -> {Orange}, Lighting -> Automatic, Mesh -> Automatic, 
   BoxRatios -> Automatic, Boxed -> False, Axes -> None];
q = RegionPlot3D[
   Sqrt[x^2 + y^2] < 1, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}, 
   PlotStyle -> {Orange}, Lighting -> Automatic, Mesh -> Automatic, 
   BoxRatios -> Automatic, Boxed -> False, Axes -> None];
Show[p, q]

Is there a way to achieve the same with the data from a list?

---

[Adaptation to thicknessFunc by @Halirutan and accompanying re-scaling]

To make the thicknessFunc more generic I adapted it to:

thicknessFunc[z_, body_, 
  b_] := (HeavisideTheta[z] - HeavisideTheta[z - b])*
   Sqrt[b^2 - (z - b)^2] + 
  b (HeavisideTheta[z - b] - 
     HeavisideTheta[z - body - b]) + (HeavisideTheta[z - body - b] - 
     HeavisideTheta[z - body - 2 b])*Sqrt[b^2 - (z - body - b)^2]

such that you can set the radius of the circular parts by setting $b$. A consequence of this is that you have to rescale the thicknessFunc in append with $1/b$ like

Append[1/b thicknessFunc[u,2]*fdata[t], u]

I don't fully understand why, but I guess it has to do with the fact that fdata is multiplied by thicknessFunc and therefore needs the straight ends of thicknessFunc to be at 1

Answer 1

This is in theory pretty simple. Think of it as two separated steps. First, you need function that models your extrusion-thickness, which has in the middle always the same value and at both ends it should round up like a circle. You can do this with Piecewise or, as I show here, with a combination of Heaviside functions:

thicknessFunc[z_, 
  body_] := (HeavisideTheta[z] - HeavisideTheta[z - 1])*
   Sqrt[1 - (1 - z)^2] + (HeavisideTheta[z - 1] - 
    HeavisideTheta[z - body - 1]) + (HeavisideTheta[z - body - 1] - 
     HeavisideTheta[z - body - 2])*Sqrt[1 - (z - body - 1)^2]

the parameter body is the size of the constant middle part. Here with the size of 2 ranging from 1 to 3:

Plot[thicknessFunc[u, 2], {u, 0, 4}]

The other part is that you can interpolate your points, so that you get a function fdata[t_] which gets a single parameter t and runs along your points for t ranging from 0 to 1 (you can actually use whatever you like here):

data = Table[(1/4 Sin[5 phi]^2 + 1) {Cos[phi], Sin[phi]}, {phi, 0, 2 Pi, Pi/50}];
With[
  {ip = ListInterpolation[#, {{0, 1}}, PeriodicInterpolation -> True] & /@ Transpose[data]},
  fdata[t_] := Through[ip[t]]
 ]

ParametricPlot[fdata[t], {t, 0, 1}]

Note that fdata[t] always returns points {x,y}. Now we turn this into a 3d function by combining the thicknessFunc with fdata. Our final function f3d will have two parameters: t which walks around the contour if increase it and u which defines our height and uses the thicknessFunc to scale the contour:

f3d[t_, u_] := Append[thicknessFunc[u,2]*fdata[t], u]

Note that only the {x,y} points of the contour are scaled and to make this work, your contour points need to lie around the zero point {0,0} as in your example. That's it, the rest is only plotting

ParametricPlot3D[f3d[t, u], {t, 0, 1}, {u, 0, 4}, Exclusions -> None, 
 PlotPoints -> 30, MaxRecursion -> 3, 
 PlotStyle -> {Orange, Specularity[White, 10]}, Axes -> None, 
 Mesh -> None]

Answer 2

How about this. Generate a list of 2D points:

pts = Table[{Cos[2 \[Pi] k/6], Sin[2 \[Pi] k/6]}, {k, 0, 6}];
ListLinePlot[pts]

and we'll use a scaling function to form the caps.

Plot[Sqrt[1 - (Abs@z - 1)^2], {z, -1, 1}, AspectRatio -> 1]
sfunc[pt_] := Module[{z = Last@pt}, Piecewise[{{pt, -1 < Last@pt < 1}}, 
  {{Sqrt[1 - (Abs@z - 1)^2], Sqrt[1 - (Abs@z - 1)^2], 1}*pt}]]

Create the extrusion

ext = Partition[Flatten@Table[sfunc[Join[#, {z}]] & /@ pts, {z, -2, 2, 0.05}], 3];

and plot it

Graphics3D@(Polygon@ext)