Condsider
function = Tan[1 x] + Tan[2 x]
Plot[function, {x, 0, 1.5}]

It has a strong discontinuity around 0.8.
The problem is , if I want to find function==0, Mathematica will not only find the real root x~1.1 , but also a artifact root x~0.8 Because I think Mathematica created a line around the discontinuity. A single point the has its y value of all values, which I call "a point that is every point".
To make this obvious, let me make a Contour Plot:
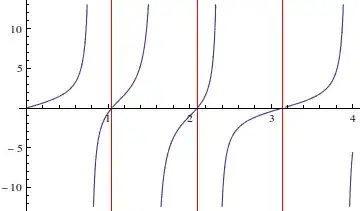
ContourPlot[function + 2*y == 0, {x, 0, 1.5}, {y, 0, 1.5}, PlotPoints -> 100]

We know that only curved line represents real roots. The constant line is the artifact. In fact, if you plot contour for function + 2*y == 1 or function + 2*y == 2, this artifact line remains. Of course, since it is a point that is every point:
ContourPlot[function + 2*y == 1, {x, 0, 1.5}, {y, 0, 1.5}, PlotPoints -> 100]
ContourPlot[function + 2*y == 2, {x, 0, 1.5}, {y, 0, 1.5}, PlotPoints -> 100]

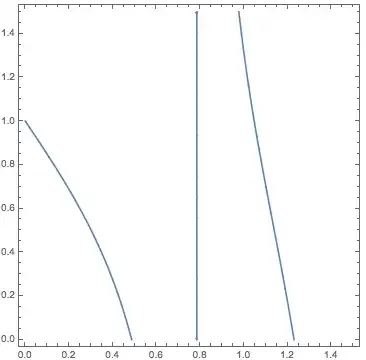
So, how to solve the problem in Contour Plot if function to plot has a strong discontinuity that Mathematica tries wrongly (hard) to connect.


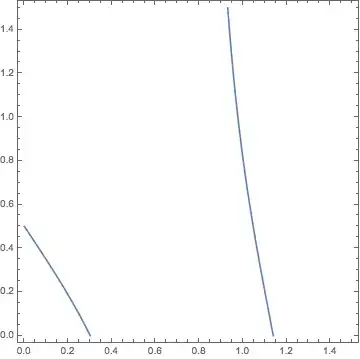

FindRoot[function[x] == 0, {x, 1}]gives the right coordinate. – Öskå Jul 27 '14 at 09:28ContourPlot[function + 2*y == 1, {x, 0, 1.5}, {y, 0, 1.5}, PlotPoints -> 100, Exclusions -> {1/function == 0}]. – b.gates.you.know.what Jul 27 '14 at 09:32