Getting rid of vertical lines in plot

Question

How can I get rid of red vertical line in below plot? Could any onehelp me?

x = 0.1;
tr = -0.0;
dp = -0.2;
xr = -0;
f = dp Cos[2 theta] + tr;
G = 8 I; 
inside = (xr + G dp x Cos[theta] Sin[theta]^2)/f^2 + (1 - 2 tr /f)^2;
lambda1 = f (1 + inside^0.5); lambda2 = f (1 - inside^0.5);
qq1 = Plot[Re[lambda1], {theta, 0, Pi}, 
   PlotStyle -> ({Red, Dashing[#]} & /@ {Large, Medium})] ;
qq2 = Plot[Re[lambda2], {theta, 0, Pi}, 
   PlotStyle -> ({Red, Dashing[#]} & /@ {Large, Medium})];

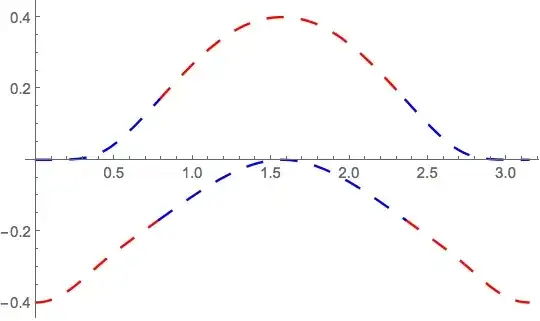
How can I get rid of red vertical line in below plot? what vertical line? I do not see one. Could you post screen shot showing what you get? here is screen shot from my PC. 11.2 on windows — Nasser, Nov 23 '17 at 19:48
I don't see a vertical line either!? I am using MMA 11.2 on Mac OS 10.11.6. Also, can not see vertical line using MMA 11.1.1 on Mac OS 10.11.6 — Joseph, Nov 23 '17 at 19:50
@Nasser. Discontinuity exclusion plotting has gotten smatter in recent versions of Mathematica. OP probably using older version. — m_goldberg, Nov 23 '17 at 19:51
A shot in the dark here: try using AxesOrigin -> {0, 0} or Axes -> False in your Plot command. — Joseph, Nov 23 '17 at 19:55
Possible duplicate of Plot draws list of curves in same color when not using Evaluate — LCarvalho, Nov 24 '17 at 17:34

Bob Hanlon · Accepted Answer · 2017-11-24T04:22:36.923

EDIT: Solution for version 10.3.1

$Version

(* "10.3.1 for Mac OS X x86 (64-bit) (December 9, 2015)" *)

x = 1/10;
tr = 0;
dp = -1/5;
xr = 0;
f = dp Cos[2 theta] + tr;
G = 8 I;
inside = (xr + G dp x Cos[theta] Sin[theta]^2)/f^2 + (1 - 2 tr/f)^2;

Separate lambda1 into its Re and Im components

lambda1 = f (1 + inside^(1/2)) // 
    ComplexExpand[#, TargetFunctions -> {Re, Im}] & // Simplify;

Extracting the Re component

lambda1Re = lambda1 /. I -> 0;

Use FunctionDomain to determine the values for the Exclusions

FunctionDomain[{lambda1Re, 0 <= theta <= Pi}, theta] //
 Simplify[#, 0 <= theta <= Pi] &

lambda2 = f (1 - inside^(1/2));

qq = Plot[{Re[lambda1], Re[lambda2]}, {theta, 0, Pi}, 
     PlotStyle -> ({#, Dashing[Large]} &) /@ {Red, Blue}, 
  Exclusions -> {-2*ArcTan[1 - Sqrt[2]], 2*ArcTan[1 + Sqrt[2]]}]

score 1 · Answer 2 · answered Nov 23 '17 at 20:19

At least for the first plot qq1 you can find coordinates of discontinuities

root1 = theta /. FindRoot[Re[lambda1], {theta, 0.8}]
root2 = theta /. FindRoot[Re[lambda1], {theta, 2.4}]

and use Exclusions to get rid of the vertical lines

qq1 = Plot[Re[lambda1], {theta, 0, Pi}, 
      PlotStyle -> ({Red, Dashing[#]} & /@ {Large, Medium}), 
      Exclusions -> {{theta == root1}, {theta == root2}}];

However I could not find roots for Re[lambda2]...

Getting rid of vertical lines in plot

2 Answers2