Merging lists and adding common elements

Question

I have two 2D arrays where some of the x-values are identical,

L={{1,1},{2,2},{3,3}};
J={{0,1},{2,2},{4,4}};

I want to add these lists in the following way

{{0,1}, {1,1},{2,4},{3,3},{4,4}};

In other words, that y-values of the data points that have the same x are added. How can I achieve this?

Please note that the arrays are not necessarily of the same length

Two arrays for test:

first = {{0.15, 0.000470185}, {0.16, 0.000521784}, {0.17, 0.000580663}, {0.18,
   0.000648083}, {0.19, 0.000725569}, {0.2, 0.000814968}, {0.21, 
  0.000918532}, {0.22, 0.00103901}, {0.23, 0.0011798}, {0.24, 
  0.00134508}, {0.25, 0.00154005}, {0.26, 0.00177121}, {0.27, 
  0.00204667}, {0.28, 0.00237667}, {0.29, 0.00277409}, {0.3, 
  0.00325523}, {0.31, 0.00384059}, {0.32, 0.00455591}, {0.33, 
  0.00543312}, {0.34, 0.00651098}, {0.35, 0.00783476}, {0.36, 
  0.00945361}, {0.37, 0.0114133}, {0.38, 0.0137402}, {0.39, 
  0.0164132}, {0.4, 0.0193217}, {0.41, 0.0222235}, {0.42, 
  0.0247384}, {0.43, 0.0264243}, {0.44, 0.0269371}, {0.45, 
  0.0261818}, {0.46, 0.024341}, {0.47, 0.0217652}, {0.48, 
  0.0188176}, {0.49, 0.0157753}, {0.5, 0.0128044}, {0.51, 
  0.00998009}, {0.52, 0.00731676}, {0.53, 0.00479353}, {0.54, 
  0.00237078}, {0.55, 0}}


second = {{-0.04, -0.0000547619}, {-0.03, -0.000405238}, {-0.02, -0.00207438}, \
{-0.01, -0.00878929}, {0, -0.0154401}, {0.01, -0.0178195}, {0.02, \
-0.0180879}, {0.03, -0.0173267}, {0.04, -0.0157714}, {0.05, \
-0.014605}, {0.06, -0.0131757}, {0.07, -0.0119764}, {0.08, \
-0.010695}, {0.09, -0.00946286}, {0.1, -0.00849357}, {0.11, \
-0.00708071}, {0.12, -0.00578286}, {0.13, -0.00468214}, {0.14, \
-0.00306119}, {0.15, -0.00146214}, {0.16, 0.00061881}, {0.17, 
  0.00194733}, {0.18, 0.00376762}, {0.19, 0.00509833}, {0.2, 
  0.00625381}, {0.21, 0.00762286}, {0.22, 0.00918905}, {0.23, 
  0.0105964}, {0.24, 0.0118067}, {0.25, 0.0134238}, {0.26, 
  0.0149774}, {0.27, 0.0163519}, {0.28, 0.017469}, {0.29, 
  0.0167517}, {0.3, 0.0102788}, {0.31, 0.00253876}, {0.32, 
  0.000314333}, {0.33, 0.000038881}, {0.34, 0.0000224524}}

first array is here: http://www.datafilehost.com/d/731a267e.

The second array I generate from this code:

factor = 11.0;
second = Table[{(38 - i)*0.01, 0}, {i, 0, 38}] - 0.04;
tempData = (1/10000) (factor/21) {
    0.41,
    0.71,
    5.74,
    46.36,
    187.70,
    305.90,
    319.0,
    298.60,
    273.50,
    245.13,
    215.60,
    193.50,
    167.80,
    139.20,
    114.20,
    93.10,
    68.80,
    35.56,
    11.30,
    -26.70,
    -55.90,
    -85.50,
    -105.60,
    -129.30,
    -155.10,
    -172.80,
    -195.30,
    -218.70,
    -240.60,
    -266.70,
    -288.00,
    -316.4,
    -330.3,
    -325.4,
    -281.95,
    -160.50,
    -37.88,
    -7.4,
    -1.0
    };

For[i = 1, i < Length[tempData] + 1, i++,
  second[[i, 2]] = tempData[[i]]];
second = second // Reverse;

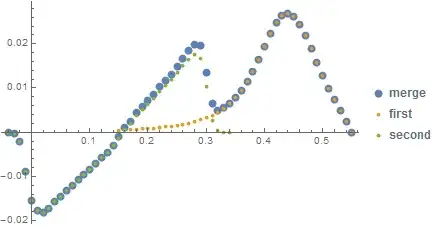
In your second example 0.17 ~= .16999999999999998. So it doesn't merge them. — Öskå, Aug 05 '14 at 13:51
@BillyJean Quick and dirty first = N@Round[first, 10^-15];. Same for second and you are all good :) — Öskå, Aug 05 '14 at 13:57
Since people keep answering duplicates we now have good answers spread across numerous Q&A's including: (4332) (16507) (26574) (43683) I encourage people to move any unique answers to the original. (Delete and repost.) — Mr.Wizard, Aug 05 '14 at 20:18

kglr · Answer 1 · 2014-08-11T12:49:04.140

8

You can also use the V10 function Merge:

List @@@ Normal @ Merge[Total][Rule @@@ Join[L, J]]

or

List @@@ Normal @ Merge[Rule @@@ Join[L, J], Total]

or (a variant of @Carlo's answer using GroupBy with a different syntax)

List @@@  Normal @ GroupBy[Join[L,J], First -> Last, Total]

to get

(* {{1, 1}, {2, 4}, {3, 3}, {0, 1}, {4, 4}}  *)

Update: Some timings using Wolfram Programming Cloud:

tstdata=RandomInteger[10,{2,100000,2}];

mergeLists[x_, y_] := Module[{f, g, l3}, f[{a_, b_}] /; NumericQ[g@a] := 
  (g[a] += b);
  f[{a_, b_}] := (g[a] := b);l3 = Join[x, y];f /@ l3;{#, g@#} & /@ Union[First /@ l3]]

(res1=mergeLists@@tstdata)//Timing //First
(* 1.889713 *)
(res2=Sort@With[{g = GatherBy[Join@@tstdata, First]},
            Thread@{DeleteDuplicates[Flatten@Map[First, g, {2}]],
            Plus @@@ Map[Last, g, {2}]}])//Timing//First
(* 0.423935 *)
(res2b=With[{g = GatherBy[Join@@tstdata, First]},
            Thread@{DeleteDuplicates[Flatten@Map[First, g, {2}]],
            Plus @@@ Map[Last, g, {2}]}])//Timing//First
(* 0.378943 *)
(res3=List @@@  Normal @ GroupBy[Join@@tstdata, First -> Last, Total])//Timing//First
(* 0.033994  *)
(res4=List@@@Normal[Total /@ GroupBy[Join@@tstdata, First -> Last]])//Timing//First
(* 0.033994 *)
(res5=List @@@ Normal @ Merge[Rule @@@ Join@@tstdata,Total])//Timing//First
(* 9.465561 *)
(res6=List @@@ Normal @ Merge[Total][Rule @@@ Join@@tstdata])//Timing//First
(* 9.496556 *)
Sort@res1==Sort@res2==Sort@res2b==Sort@res3==Sort@res4==Sort@res5==Sort@res6
(* True *)

edited Aug 11 '14 at 12:49

answered Aug 05 '14 at 14:08

kglr

394,356
18
477
896

Nice! Could you provide some comparison indicator for those of us without v10 available? Perhaps just comparing with any other answer to this question... – Dr. belisarius Aug 05 '14 at 14:38
@eldo, thanks!! – kglr Aug 05 '14 at 14:48
@belisarius, good idea -- I will update with some timings. – kglr Aug 05 '14 at 14:50
@kguler When will you update with some timings? :P – Öskå Aug 11 '14 at 11:50
@Oska, apologies for the delay to post timings -- I do not have the desktop version of V10 yet; I have been using Wolfram Programming Cloud and my internet connection has been too slow recently to do a decent timing experiment. BTW, if you have desktop V10 i would appreciate it very much if you could post your timing results. – kglr Aug 11 '14 at 11:58
Alas I have v8.. :) Maybe @belisarius can do it? :) – Öskå Aug 11 '14 at 12:01
@Öskå Still v9 here ;D – Dr. belisarius Aug 11 '14 at 12:33
@belisarius Meh, I thought you wrote some fancy v10 answers. I guess you all use the cloud :) – Öskå Aug 11 '14 at 12:36
@Oska, belisarius , I just added some timings. – kglr Aug 11 '14 at 12:44

Dr. belisarius · Answer 2 · 2014-08-05T13:52:16.837

5

Just showing some tricks:

l1 = {{1, 1}, {8, 2}, {3, 3}};
l2 = {{0, 1}, {8, 3}, {4, 4}};

mergeLists[x_, y_] := Module[{f, g, l3},

  f[{a_, b_}] /; NumericQ[g@a] := (g[a] += b);
  f[{a_, b_}] := (g[a] := b);

  l3 = Join[x, y];
  f /@ l3;
  {#, g@#} &/@ Union[First /@ l3]
  ]

(*{{0, 1}, {1, 1}, {3, 3}, {4, 4}, {8, 5}}*)

edited Aug 05 '14 at 13:52

answered Aug 05 '14 at 12:47

Dr. belisarius

115,881
13
203
453

wow, this is fast. You time 0.298017, eldo's time 4.371250 – molekyla777 Aug 05 '14 at 12:51
@molekyla777 eldo's answer uses Replacement rules, which are usually slow – Dr. belisarius Aug 05 '14 at 12:52
This only works if the arrays are of the same size – BillyJean Aug 05 '14 at 12:54
Sorry, you are right. Also works for non-equal lengths – BillyJean Aug 05 '14 at 12:56
@belisarius It doesn't work with my data set, I pasted the two arrays in the OP – BillyJean Aug 05 '14 at 13:01
1

@Öskå Could you please try it now again? – Dr. belisarius Aug 05 '14 at 13:30
1

@belisarius Perfect. Or we are both wrong :P – Öskå Aug 05 '14 at 13:35
@belisarius It works now, but 0.17 and 0.18 are not added, just like in the other answer. When I import the data set from external files they are not added, when I write the arrays in explicitly they are added (?!) – BillyJean Aug 05 '14 at 13:36
@belisarius Could you help me understand your code better, perhaps with some elaborations on the steps you made? I feel like this is a very clever piece of code, but I'm not smart/advanced enough to know what's going on there. – seismatica Aug 05 '14 at 13:38
@seismatica The style is already explained in a previous answer by Mr.Wizard with comments done by me (or was it the other way?) I'll try to find the original link – Dr. belisarius Aug 05 '14 at 13:45
@BillyJean Sounds like a rounding or numerical format problem to me – Dr. belisarius Aug 05 '14 at 13:47
@belisarius Would really appreciate it if you do! – seismatica Aug 05 '14 at 13:59
@seismatica I can't find it,but perhaps executing the following code may enlighten you f[{a_, b_}] := (g[a] := Print["I was defined as " <> ToString@b]); f[{1, 2}]; f[{3, 4}]; ?g – Dr. belisarius Aug 05 '14 at 14:25
@seismatica and belisarius: is this perhaps what you were referring to? There are no comments there but it is a related answer to a related question. – Mr.Wizard Aug 05 '14 at 22:31
@Mr.Wizard Thanks, but it wasn't that one. If I remember well, the answer was yours and I commented to improve it on a similar structure I used here. But I can't remember the main question theme, so it's almost impossible for me to find. – Dr. belisarius Aug 05 '14 at 23:01

Öskå · Accepted Answer · 2014-08-05T13:34:22.673

4

Once again not very fancy but it does the job:

L = {{1, 1}, {2, 2}, {3, 3}};
J = {{0, 1}, {2, 2}, {4, 4}};
Sort@With[{g = GatherBy[Join[L, J], First]}, 
  Thread@{DeleteDuplicates[Flatten@Map[First, g, {2}]], 
          Plus @@@ Map[Last, g, {2}]}]

{{0, 1}, {1, 1}, {2, 4}, {3, 3}, {4, 4}}

With the data provided by the OP and res = Sort[With[{..., Join[first, second]...] one can have:

ListPlot[{res, first, second}, 
  PlotStyle -> {Directive[{PointSize@.02, Red}], Blue, Green},
  Filling -> Axis, Axes -> {False, True}]

Mathematica graphics

edited Aug 05 '14 at 13:34

answered Aug 05 '14 at 12:21

Öskå

8,587
4
30
49

When I try this method with the two arrays in the OP, the points around 0.15 are not added – BillyJean Aug 05 '14 at 13:10
@BillyJean They are. See here. – Öskå Aug 05 '14 at 13:12
But if I use ListLinePlot on the array, I can see that there are multiple values. But if I show the array using MatrixForm, then I can see there aren't multiple values?! – BillyJean Aug 05 '14 at 13:15
@BillyJean Try with a new kernel? Works like a charm for me and all the data seems to be added. – Öskå Aug 05 '14 at 13:20
It's at 0.17 and 0.18, I see it in both the plot and the data – BillyJean Aug 05 '14 at 13:22
@BillyJean What about 0.17 and 0.18? It works fine for me. See here. – Öskå Aug 05 '14 at 13:25
When I import the data set from external files they are not added, when I write the arrays in explicitly they are added (?!). Odd. – BillyJean Aug 05 '14 at 13:36
@BillyJean Feel free to upload your external file somewhere so one can test. Probably nothing to worry about. – Öskå Aug 05 '14 at 13:39
@Öskå Please see updated OP. One array I generate from an extenral file (upload link provided), the second array I generate using shown code. – BillyJean Aug 05 '14 at 13:44

score 4 · Answer 4 · answered Aug 05 '14 at 13:53

4

A somewhat shorter way of achieving the same on V10:

merge = Total /@ GroupBy[Join[first, second], First -> Last]

This would return an Association, but you can still use it in ListPlot. If you don't want an Association

List @@@ Normal[merge]

answered Aug 05 '14 at 13:53

Carlo

1,171
9
12

score 3 · Answer 5 · answered Aug 05 '14 at 12:39

3

L = {{1, 1}, {2, 2}, {3, 3}};
J = {{0, 1}, {2, 2}, {4, 4}};

Sort@Flatten[Transpose[{J, L}] /. {{a_, b_}, {a_, c_}} :> {{a, b + c}}, 1]

{{0, 1}, {1, 1}, {2, 4}, {3, 3}, {4, 4}}

answered Aug 05 '14 at 12:39

eldo

67,911
5
60
168

That's fancy :) and smarter :P – Öskå Aug 05 '14 at 12:41
@Öskå Thanks - shouldn't be the fastest though for large lists :) – eldo Aug 05 '14 at 12:43
Only works for two list with no duplicate first entries. – John McGee Aug 05 '14 at 12:44
@John Could you give an example? – eldo Aug 05 '14 at 12:56
l = {{1, 1}, {2, 2}, {2, 7}, {3, 3}}; j = {{0, 1}, {2, 5}, {4, 5}, {4, 1}}; – John McGee Aug 05 '14 at 13:02
This following slight change seems more general. Sort@Flatten[Transpose[{l, j}], 1] //. {x___, {a_, b_}, {a_, c_}, y___} :> {x, {a, b + c}, y} – John McGee Aug 05 '14 at 13:03
@JohnMcGee oops I didn't see your answer before I posted mine! Why not using Join instead of Transpose and Flatten? – seismatica Aug 05 '14 at 13:13

score 2 · Answer 6 · answered Aug 05 '14 at 12:52

2

Sow, Reap implementation

t = Join[L, J];
tags = DeleteDuplicates[t[[All, 1]]];
res = Reap[t /. {x_, y_} :> {Sow[y, x]}][[2]];
MapThread[{#1, Total@#2} &, {tags, res}]
(*{{1, 1}, {2, 4}, {3, 3}, {0, 1}, {4, 4}}*)

answered Aug 05 '14 at 12:52

molekyla777

2,888
1
14
28

More terse: Reap[Sow@@@Join[J,L],_,{#1,Total@#2}&]//Last – Simon Woods Aug 05 '14 at 17:23

seismatica · Answer 7 · 2014-08-05T13:27:53.513

2

One-liner:

Sort@Join[L,J]//.{a___,{x_,y1_},{x_,y2_},b___}:>{a,{x,y1+y2},b}

Testing it on your 2 lists (took about 0.001 in AbsoluteTiming)

merge=Sort@Join[first,second]//.{a___,{x_,y1_},{x_,y2_},b___}:>{a,{x,y1+y2},b};
ListPlot[{merge,first,second},
PlotLegends->{"merge","first","second"},PlotStyle->AbsolutePointSize/@{8,4,4}]

Mathematica graphics

edited Aug 05 '14 at 13:27

answered Aug 05 '14 at 13:11

seismatica

5,101
1
22
33

score 1 · Answer 8 · answered Aug 05 '14 at 12:38

1

Here is an optional approach with more details. First merge the lists then gather the first coordinates

t = Flatten[{l, j}, 1]; f = Union[First[[Transpose[t]]];

Next form a ragged array, collecting by the first element.

r = Cases[t, {#, _}] & /@ f;

Finally collapse the ragged array by summing

Total[#[[All, 2]]] & /@ r; rstl=Transpose[{f,s}];

I hope that you find this helpful.

answered Aug 05 '14 at 12:38

John McGee

2,538
11
15

Thanls, but this only works if the arrays are of the same size – BillyJean Aug 05 '14 at 12:55

Merging lists and adding common elements

8 Answers8

Linked

Related