4

I am playing around with the Manipulate sentence. I think the following code is right, and actually Mathematica 9.0 doesn't return any error message, but I am observing something strange:

  • when I execute the Manipulate sentence, the fan of my laptop starts overworking (I do not know if this expression is right) making lot of noise, which usually means that there is a heavy process running, and if I delete the result of the code, the fan returns to its normal state; and

  • the vertical line at the right of the result of the code is highlighted in black and slightly twinkling.

This is the code:

Manipulate[f[x_] := Sin[x]; {Plot[f[x], {x, 0, a}], f[a]}, {a, 1, 50}]

And this is the image of what I get, where you can see the black vertical line:

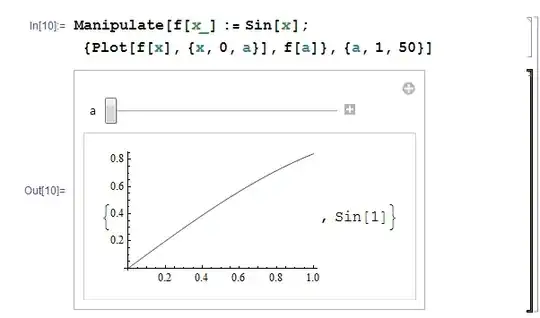
Manipulate causing computer strange behaviour

So, my question is: do you get the same computer behaviour, or is it just me? And, is there something wrong with this piece of code?

Vicent
  • 1,101
  • 6
  • 16
  • 1
    Related: http://mathematica.stackexchange.com/questions/49257/problems-with-manipulate-indicated-by-blinking-output-cell/49264#49264 – eldo Aug 06 '14 at 12:39

3 Answers3

8

Your code is redefining the function f every time the Manipulate updates its contents pane, which causing Mathematica to go hyper.

You should use the option Initialization so the function is defined just once.

Manipulate[
  Column @ {Plot[f[x], {x, 0, a}], f[a]},
  {a, 1, 50},
  Initialization :> (f[x_] = Sin[x])]

manip

m_goldberg
  • 107,779
  • 16
  • 103
  • 257
  • 1
    Ok, let me try to get this straight: The front-end tells Manipulate to re-evaluate its first argument whenever one of the symbols in it (or at least one of those tracked) changes definition. In the OP's case, this re-evaluation of the first argument causes f to change definition, leading to a never ending loop of misery. (Oh, and +1 for Initialization btw). – Teake Nutma Aug 06 '14 at 18:05
  • 1
    @TeakeNutma. You got it. The reason edo's approach calms things down is because, when f is no longer tracked, there is no infinite recursion. But it's not the best fix because it still re-evaluates f on each update of the contents pane. – m_goldberg Aug 07 '14 at 02:04
  • @m_goldberg I'm working with complicated Manipulates involving tables with 30.000 rows times 20 columns. All of my functions are outside Manipulate. 20 constants are globally defined, 30 variables are "tracked". If I would move all my 40 functions to Initialization I couldnt read my code anymore. IMOTrackedSymbols` works in an extremely fast and reliable manner. – eldo Aug 07 '14 at 02:58
  • @eldo. I do not argue against the controlling the tracking of symbols. Nor do I argue against defining functions outside a Manipulate expression. But it is always a bad idea to have a function definition as part of the *first* argument to Manipulate, even when you use the TrackedSymbols option to suppress recursive evaluation. The SetDelayed expression defining the function will still be evaluated once each time the contents pane is refreshed. – m_goldberg Aug 07 '14 at 03:15
  • @m_goldberg Agree – eldo Aug 07 '14 at 03:23
4
Manipulate[f[x_] := Sin[x]; {Plot[f[x], {x, 0, a}], f[a]}, {a, 1, 50},
  TrackedSymbols :> {a}]

solved the problem for me (I got the same flickering). The Documentation doesn't say too much about TrackedSymbols. In your case not only a but also x is continiously updateted. But Manipulate should update x only in case a changes, i.e., the slider is moved. This you specify by limiting TrackedSymbols to a.

eldo
  • 67,911
  • 5
  • 60
  • 168
2

It seems the definition of f inside the Manipulate is causing the problem (I'm not sure on the exact details, perhaps someone else can elaborate). Besides eldo's solution with TrackedSymbols, you might opt to define f outside:

f[x_] := Sin[x]
Manipulate[{Plot[f[x], {x, 0, a}], f[a]}, {a, 1, 50}]

But why define f at all? It can also be done without specifying f:

Manipulate[{Plot[Sin[x], {x, 0, a}], Sin[a]}, {a, 1, 50}]

Note that if you want the Sin to keep being displayed as Sin on the RHS of the plot, you can do the following:

Manipulate[{Plot[Sin[x], {x, 0, a}], With[{a = a}, HoldForm@Sin[a]]}, {a, 1, 50}]

Mathematica graphics

On Mathematica 10, the following should also work (haven't checked though):

Manipulate[{Plot[Sin[x], {x, 0, a}], Inactive[Sin][a]}, {a, 1, 50}]
Community
  • 1
Teake Nutma
  • 5,981
  • 1
  • 25
  • 49