Tutorial on how to overuse Mathematica
Take this as a humorous example of what the usual Mathematica approach looks like. A Goldberg machine of code, so to speak.
Since this is quite a lengthy answer with code pieces spread all over it, making it very inconvenient for copy+paste, I've uploaded the corresponding .nb. You can download it here.
1. Establishing the equation
Establishing is Hebrew and stands for do until happy with trial and error. Trial and error here means coding a clock, which will give us valuable information about the system, for example whether the clock hands meet at all at some point.
polar is a wrapper generating polar coordinates: it maps the interval $[0,1)$ to coordinates on the unit circle.
minute/hour then use this map to calculate where the clock's hands should point to: the minute (or hour) hand travels around the circle once in $60$ (or $12\cdot60$) minutes, therefore the parameter is divided by those numbers, making them maps from $[0,60)$ (or $[0,12\cdot60)$) to the unit circle. ticks is the same thing again, only that the ticks should "travel" around the clock once only per half day, which yields a divisor of $12$.
polar[t_] := Through[{Cos,Sin}[-2\[Pi] t+\[Pi]/2]]
minute = polar[#/60]&;
hour = polar[#/(12 60)]&;
ticks = polar[#/12]&;
Manipulate[
Graphics@Flatten@{
Circle[],
Text[#, 1.1 ticks[#]]& /@ Range[12],
Line[{0.9 ticks[#], ticks[#]}]& /@ Range[12],
Gray, Thickness[.025], Arrowheads[.1], Arrow[{{0, 0}, 0.7 hour[t]}],
Black, Thickness[.01], Arrowheads[.05], Arrow[{{0, 0}, minute[t]}]
},
{{t, 0, "Time\n(minutes after midnight)"}, 0, 12*60}
]
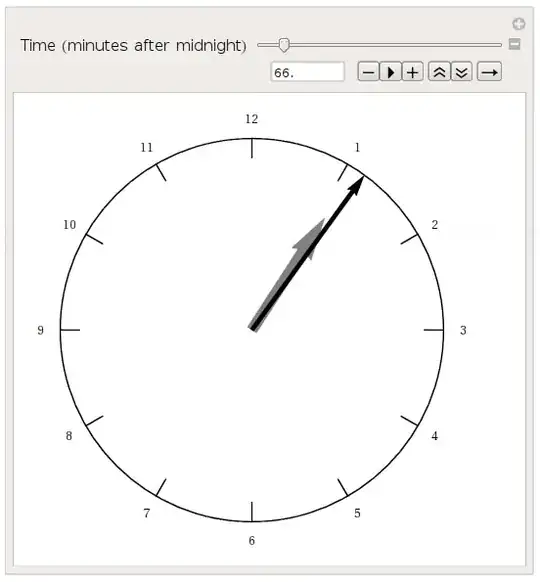
After countless hours of experimentation, I was finally able to determine a position in which (up to numerical precision) the hands did indeed overlap.
2. Solving the system
The bad news is that I have no sense of reason (12/11 hour etc), luckily there's Mathematica at my hand. Let's generate the equations ...
eqns = Thread[minute[t] == hour[t]]
{ Sin[(Pi t)/30] == Sin[(Pi t)/360],
Cos[(Pi t)/30] == Cos[(Pi t)/360] }
Wonderful! Solve it!
intersections = Sort[t /. FullSimplify@Solve[Flatten@{eqns, 0 <= t < 12 60}, t]]
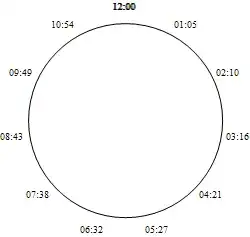
{0, 720/11, 1440/11, 2160/11, 2880/11, 3600/11, 4320/11, 5040/11, 5760/11, 6480/11, 7200/11}
3. Displaying the results
This result doesn't look much like something a normal person would have his watch display. Let's change that.
dates = DatePlus[{2012,1,23}, {#, "Minute"}]& /@ intersections;
DateString[#, {"Hour", ":" , "Minute", ":", "Second"}]& /@ dates
{00:00:00, 01:05:27, 02:10:54, 03:16:21, 04:21:49, 05:27:16, 06:32:43, 07:38:10, 08:43:38, 09:49:05, 10:54:32}
To make a nice graphical representation of what a watch with 22 fingers looks like, we can simply strip the Manipulate code given above a bit, add multiple hour/minute hands in return, and combine it all into a single graphic:
Graphics@Flatten@{
Circle[],
Text[#, 1.1 ticks[#]]& /@ Range[12],
Line[{0.9 ticks[#], ticks[#]}]& /@ Range[12],
Gray, Thickness[.025], Arrowheads[.1], Arrow[{{0, 0}, 0.7 hour[#]}]& /@ intersections,
Black, Thickness[.01], Arrowheads[.05], Arrow[{{0, 0}, minute[#]}]& /@ intersections
}
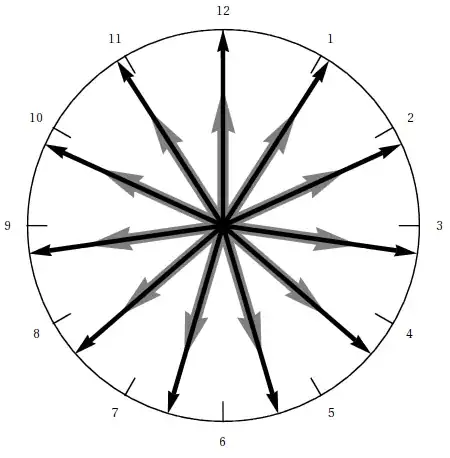
Done. :-)
3. The take away message
- Mathematica is fun.
- Mathematica can also be useful.
- There are two headlines numbered $3$.
FullSimplify is incredibly powerful.- Simple riddles may expand to (arguably) interesting problems when done with sufficient mathematical rigor
(polar equations for a clock, seriously?!)