To inscribe a circle in a given triangle

Question

I am trying to to inscribe a circle in a given triangle but it isn't working. I've used GeoGebra with this construction and worked but as I'm new to Mathematica, I am missing something. It can't be so complex to do. Here is my code:

pA = {0, 0}; pB = {1.1, 1}; pC = {1.5, 0};
midAB = (pA + pB)/2; midBC = (pB + pC)/2; midAC = (pA + pC)/2;
myT = Triangle[{pA, pB, pC}];
centerC = (midAB + midBC + midAC)/3
raioC = Last[centerC]
Graphics[{EdgeForm[Directive[Thick, Blue]], White, 
  myT, {PointSize[Large], Red, Point[midBC]}, {PointSize[Large], Red, 
   Point[pA]},
  {Orange, Line[{pA, midBC}]},
  {Orange, Line[{pB, midAC}]},
  {Orange, Line[{pC, midAB}]},
  {Red, Circle[centerC, Last[centerC]]},
  }, AspectRatio -> Automatic, PlotRange -> All]

I understand that I'm not doing right the radius of the circle but I've tried more than one way to do that.

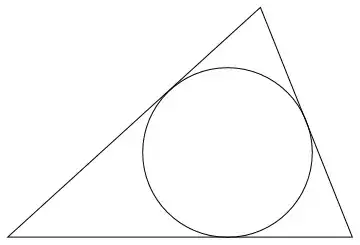
Here is the original (book) construction:

To construct: The circle inscribed in $\triangle ABC$

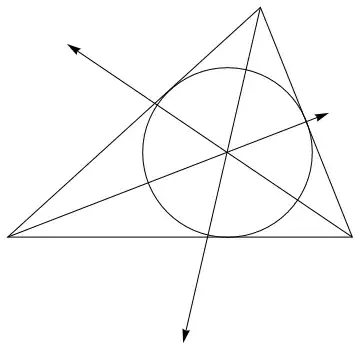
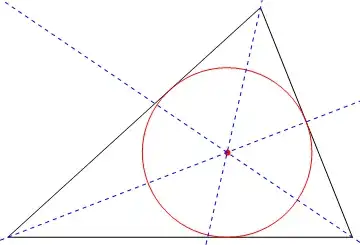
Construction: Construct the bisectors of two of the angles of $\triangle ABC$. Their intersection is the center of the required circle, and the distance (perpendicular) to any side is the radius. (Any point on the bisector of an angle is equidistant from the sides of the angle.)

As I said, it worked in GeoGebra and it is almost working with my code. Thank you for any help.

Thank you all for the help, all the answers are fine. – Luiz Meier Aug 21 '14 at 02:06 — Luiz Meier, Aug 21 '14 at 02:06

score 20 · Answer 1 · answered Aug 21 '14 at 01:35

version 10

pA = {0, 0}; pB = {1.1, 1}; pC = {1.5, 0};
lr = MeshRegion[{pA, pB, pC}, Triangle[Range@3]];
r1 = RegionDistance[InfiniteLine[{pA, pB}], {x, y}];
r2 = RegionDistance[InfiniteLine[{pB, pC}], {x, y}];
r3 = RegionDistance[InfiniteLine[{pC, pA}], {x, y}];
centerC = {x, y} /. NSolve[{r1 == r2, r2 == r3}, {x, y}, Reals];
centerC = Select[centerC, RegionMember[lr, #] &][[1]]
raioC = RegionDistance[Line[{pA, pB}], centerC]
Graphics[{
  EdgeForm[{Thick, Blue}], White, Triangle[{pA, pB, pC}],
  PointSize[Large], Red, Point@centerC,
  Red, Circle[centerC, raioC]}
 ]

{0.954787, 0.369127}

0.369127

enter image description here

Nice V10 demonstration of a new functionality +1. – PlatoManiac Aug 21 '14 at 07:44 — PlatoManiac, Aug 21 '14 at 07:44

C. E. · Accepted Answer · 2014-08-21T01:50:41.197

As KennyColnago has observed your equations seem to be off but there is another way of determining the incircle. I'd already typed it up with sources that may be helpful so let's post it, even if it's the same thing.

{a, b, c} = {Norm[pC - pB], Norm[pA - pC], Norm[pA - pB]};
area = With[{s = (a + b + c)/2}, Sqrt[s (s - a) (s - b) (s - c)]];
r = 2 area/(a + b + c);
incenter = (a pA + b pB + c pC)/(a + b + c);

Graphics[{
  EdgeForm[Black], White, Triangle[{pA, pB, pC}],
  Black, Point[incenter],
  Circle[incenter, r]
  }]

Incircle

The formula for the coordinates of the incenter can be found here, the relationship between the radius and the area is discussed here and the area is calculated with Heron's formula found here.

It's also worth noting that we can "cheat" with Mathematica 10:

incenter = {a, b, c}.{pA, pB, pC}/ArcLength[Line[{pA, pB, pC, pA}]];
r = 2 Area[Triangle[{pA, pB, pC}]]/ArcLength[Line[{pA, pB, pC, pA}]];

Although this sort of cheating is not as outrageous as that by Junho Lee of course ;)

score 14 · Answer 3 · edited Aug 21 '14 at 04:25

The incircle of a triangle may be calculated as follows.

InCircle[{x1_, y1_}, {x2_, y2_}, {x3_, y3_}] := 
   With[{
      a = Norm[{x2,y2} - {x3,y3}], 
      b = Norm[{x3,y3} - {x1,y1}], 
      c = Norm[{x1,y1} - {x2,y2}]}, 
   Circle[(a {x1, y1} + b {x2, y2} + c {x3, y3})/(a + b + c), 
          1/2 Sqrt[-(((a - b - c) (a + b - c) (a - b + c))/(a + b + c))]]]

For your example points, InCircle[{0,0},{1.1,1},{1.5,0}] produces Circle[{0.954787, 0.369127}, 0.369127], which may be plotted with

Graphics[{
   Line[{{0, 0}, {1.1, 1}, {1.5, 0}, {0, 0}}],
   Red, Thick, InCircle[{0, 0}, {1.1, 1}, {1.5, 0}]}]

Mathematica graphics

chyanog · Answer 4 · 2014-08-28T13:17:35.853

inCircle[p_] := 
  Circle[{x, y}, Abs@r] /. 
   Solve[((# - #2).{y, -x} - Det@{##})/Norm[# - #2] & @@@ 
      Subsets[p, {2}] == r {1, -1, 1}];

Manipulate[
 Graphics[{Line@p[[{1, 2, 3, 1}]], Red, inCircle@p}, PlotRange -> 6, 
  Frame -> 1], {{p, {{-2, -1}, {3, -2}, {0, 3}}}, Locator}]

Another inCircle:

inCircle[pt : {v1_, v2_, v3_}] :=
 Block[{a, b, c, p},
  {a, b, c} = Norm /@ {v2 - v3, v3 - v1, v1 - v2};
  p = (a + b + c)/2;
  Circle[{a, b, c}.pt/(2 p),  Sqrt[p (p - a) (p - b) (p - c)]/p]]

enter image description here

score 8 · Answer 5 · edited Apr 13 '17 at 12:55

Although Insphere[] is now built-in, I would still like to present an alternative technique, used in this previous answer. The idea, due to Miroslav Fiedler, is to use the inverse of the Cayley-Menger matrix to determine the inradius and incenter. (Some more algebraic effort will yield the circumradius and circumcenter as well.)

The routine CayleyMengerMatrix[] in the previous answer can now be slightly improved with the new function DistanceMatrix[]:

CayleyMengerMatrix[pts_?MatrixQ] /; Subtract @@ Dimensions[pts] == 1 :=
     ArrayFlatten[{{0, 1},
                   {1, DistanceMatrix[pts, DistanceFunction -> SquaredEuclideanDistance]}}]

CircumInSphere[pts_?MatrixQ] /; Subtract @@ Dimensions[pts] == 1 := 
       Module[{cv, icm, iv, rc},
              icm = -2 Inverse[CayleyMengerMatrix[pts]]; cv = icm[[1, 2 ;;]];
              {rc, iv} = Through[{First, Rest}[Sqrt[Tr[icm, List]]]];
              {{cv.pts/Total[cv], rc/2}, {iv.pts, 1}/Total[iv]}]

Now, generate the incircle:

tri = {{0, 0}, {11/10, 1}, {3/2, 0}};
is = Circle @@ Last[CircumInSphere[tri]] // FullSimplify
   Circle[{1/20 (15 - 2 Sqrt[29] + Sqrt[221]), 15/(15 + 2 Sqrt[29] + Sqrt[221])},
          15/(15 + 2 Sqrt[29] + Sqrt[221])]

Graphics[{Directive[{EdgeForm[Black], FaceForm[]}], Polygon[tri], is}]

triangle and incircle

Displaying the angle bisectors is not too hard:

bisectors = With[{ab = 1.5 (* arbitrary scaling *)
                  Normalize[Total[Map[Composition[Normalize,
                                                  TranslationTransform[-#[[2]]]], 
                                      Delete[#, 2]]]]},
                 Arrow[{#[[2]], #[[2]] + ab}]] & /@ 
            Partition[tri, 3, 1, 1];

Graphics[{Directive[{EdgeForm[Black], FaceForm[]}], Polygon[tri], is, bisectors}]

with bisectors

score 5 · Answer 6 · answered Jan 07 '18 at 21:55

5

(For completeness, an answer using Insphere)

As mentioned by @JM, in M10.2+ you can use Insphere:

pA = {0, 0}; pB = {1.1, 1}; pC = {1.5, 0};

Insphere[{pA, pB, pC}]

Sphere[{0.954787, 0.369127}, 0.369127]

in agreement with the other answers.

answered Jan 07 '18 at 21:55

Carl Woll

130,679
6
243
355

Syed · Answer 7 · 2023-12-12T16:41:08.800

Using TriangleCenter and TriangleMeasurement and AngleBisector:

(* all introduced April 16, 2019)

Clear["Global`*"];
pA = {0, 0}; pB = {1.1, 1}; pC = {1.5, 0};
tri = Triangle[{pA, pB, pC}];
c = TriangleCenter[tri, "Incenter"];
r = TriangleMeasurement[tri, "Inradius"];
Graphics[{
  FaceForm[None], EdgeForm[Thin]
  , tri
  , Red, Circle[c, r]
  , AbsolutePointSize[6], Point@c
  (* --- Angle bisectors *)
  , Blue, Dashed
  , AngleBisector[{pB, pA, pC}]
  , AngleBisector[{pA, pB, pC}]
  , AngleBisector[{pA, pC, pB}]
  }]

To limit the bisectors to triangle, use the following variation for each of the bisectors:

RegionIntersection[AngleBisector[{pB, pA, pC}], tri]

score 2 · Answer 8 · answered Dec 12 '23 at 16:50

`TriangleConstruct`

Manipulate[
 Graphics[{Style[Triangle[p], Opacity[0.2]], 
   TriangleConstruct[p, "Incircle"], Red, Dashed, 
   MapApply[HalfLine]@TriangleConstruct[p, {"AngleBisector", All}]}, 
  PlotRange -> 6], {{p, {{-2, -1}, {3, -2}, {0, 3}}}, Locator}]

WolframLanguageData["TriangleConstruct", {"VersionIntroduced", "DateIntroduced"}]

score 1 · Answer 9 · answered Dec 12 '23 at 17:42

1

One more approach:

GeometricScene[{a -> {0, 0}, b -> {1.1, 1},  c -> {1.5, 0}}, 
{Triangle[{a, b, c}],Insphere[Triangle[{a, b, c}]]}]

answered Dec 12 '23 at 17:42

user64494

26,149
4
27
56

To inscribe a circle in a given triangle

9 Answers9

`TriangleConstruct`

Linked

Related