How to apply a trigonometric identity to a formula

Question

The product of cosines is given by (Wikipedia):

$ \prod_{k=1}^{n} \cos{\theta_k} = \frac{1}{2^n}\sum_{e\in S} \cos(e_1\theta_1+\ldots+e_n\theta_n) $

where $S={1,-1}^n$.

How can I apply this to a formula in Mathematica, say the formula:

$ \cos{n_1}+\cos{n_2}+\cos{n_3}\cos{n_4}+\cos{n_5}\cos{n_6}\cos{n7} $

Answer 1

I think Artes comment is the best answer to this question.

I post this just as a way to play with this identity. f will take a product of Cos and return sum. I have not tried to pattern search for parts of expressions.

f[exp_] := 
 With[{v = Cases[{exp}, Cos[x_] :> x, Infinity]}, 
  Total[Cos[v.#] & /@ Tuples[{1, -1}, Length[v]]]/2^Length[v]]

You can do some testing (NOT PROOF obviously):

h[m_] := With[{var = Table[Unique["x"], {Length@m}]}, 
  f[Times @@ (Cos[#] & /@ var)] /. Thread[var -> m]]
cosp[m_] := Times @@ (Cos /@ m)

Tests:

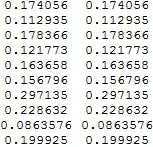
test = RandomReal[{0, 1}, {10, 10}];
Grid[Through[{h, cosp}[#]] & /@ test]

Symbolic:

cosp[{n1, n2, n3}]

gives Cos[n1] Cos[n2] Cos[n3]

h[{n1, n2, n3}]

gives: 1/8 (2 Cos[n1 - n2 - n3] + 2 Cos[n1 + n2 - n3] + 2 Cos[n1 - n2 + n3] + 2 Cos[n1 + n2 + n3])

`and

TrigExpand[h[{n1, n2, n3}]]

gives:

Cos[n1] Cos[n2] Cos[n3]