2

In the following example, $u(x)$ is found numerically using NDSolve method. 

 F = 1/1000
    h = 12000/1000
    d = 10/10
    L = 1000
    W = 3
    phi[x_] := 
     Piecewise[{{(1/2)*(1 - Tanh[((L*x)/(d))]), 
        x <= 1/2}, {(1/2)*(1 + Tanh[((L*(x - L/L))/(d))]), x > 1/2}}]
    vE[x_] := x*(1 - x)*4
    s = NDSolve[{u''[x] == (h*L*L/(d*d))*phi[x]*phi[x]*u[x] - 
         F*L*L*(1 - phi[x]), u[-W*d/L] == 0, u[1 + W*d/L] == 0}, 
      u, {x, -W*d/L, 1 + W*d/L}, Method -> "StiffnessSwitching", 
      WorkingPrecision -> 40, InterpolationOrder -> All]
    diff[x_] := (u[x] - vE[x])*(u[x] - vE[x])
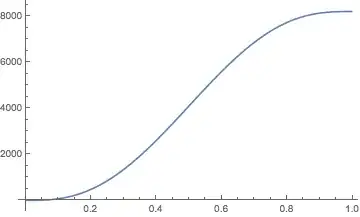
    Plot[Evaluate[{diff[x]} /. s], {x, W*d/L, 1 - W*d/L}, 
     PlotRange -> All]

Which works perfectly. I need to see what is mean square error between obtained solution and another function $vE(x)$. 

sum = 0;
Do[
 first = W*d/L;
 second = 1 - W*d/L;
 {sum = sum + diff[first + (i/100)*(second - first)]},
 {i, 0, 100, 1}]
Evaluate[sum]

but this gives only expression but not value. I think this is because $u(x)$ is obtained at discrete points only and is not defined on the points on which I have calculated error. I also tried using integration,

intVal = NIntegrate[({u[x]} /. s - vE[x])*({u[x]} /. s - vE[x]), {x, 
   W*d/L, 1 - W*d/L}]

but this gives long error message ending with,

 "...is neither a list of replacement rules nor a valid dispatch table, and so cannot be used for replacing"

How can I evaluate this integral?

alekhine
  • 429
  • 2
  • 7
  • Evaluate[sum] gives number if you use diff[x_] := (u[x] - vE[x])*(u[x] - vE[x])/.s. Then NIntegrate[diff[x], {x, W*d/L, 1 - W*d/L}] works too. The current problem for your NIntegrate is that - has lower precedence than /., which you can easily check out by selecting the code click by click – Coolwater Sep 03 '14 at 19:26
  • on thing to note NDSolve returns a list of solutions, even though in this case there is only one solution, so you should be doing /. s[[1]]. (as is you get a bunch of superfluous {} in the results ) – george2079 Sep 03 '14 at 20:45
  • @Coolwater, it worked with your suggestion, thanks.. – alekhine Sep 04 '14 at 08:09

1 Answers1

2

You can integrate the mean square error mse at the same time as computing u[x].

s = NDSolve[{
    u''[x] == (h*L*L/(d*d))*phi[x]*phi[x]*u[x] - F*L*L*(1 - phi[x]),
    u[-W*d/L] == 0, u[1 + W*d/L] == 0,
    mse'[x] == (u[x] - vE[x])^2, mse[-W*d/L] == 0},
   {u, mse}, {x, -W*d/L, 1 + W*d/L}, Method -> "StiffnessSwitching", 
   WorkingPrecision -> 40, InterpolationOrder -> All];

 Plot[Evaluate[mse[x] /. s], {x, W*d/L, 1 - W*d/L}, PlotRange -> All]

Mathematica graphics

You seem to be interested in this change:

mse[1 - W*d/L] - mse[W*d/L] /. First@s

(* 8198.070964448656291179158359833465311096 *)

The problem with the code

 intVal = NIntegrate[({u[x]} /. s - vE[x])*({u[x]} /. s - vE[x]), {x, W*d/L, 1 - W*d/L}]

is a syntax issue. The expression that /. tries to apply is s - vE[x]. This can be seen from the TreeForm of the expression:

Hold[({u[x]} /. s - vE[x])] // TreeForm

Mathematica graphics

In other words, ReplaceAll has lower precedence than Plus (represented by the minus sign). The proper code is

intVal = NIntegrate[((u[x] /. First@s) - vE[x])^2, {x, W*d/L, 1 - W*d/L},
  WorkingPrecision -> 40]

(* 8198.070964448656291179224357022321689725 *)
Michael E2
  • 235,386
  • 17
  • 334
  • 747